Quaternion representation
Quaternions are considered to be a scalar value and a 3D bivector algebra value. Since, in 3D, vector and bivector algebras are virtually identical we can use quaternions to calculate reflections.
Since this only works in 3D and since it can't be combined with other types of transform it is more of a curiosity than a useful technique.
We can represent reflection using quaternions as explaind here. To reflect the point Pin we use the formula Pout = q * Pin * q.
In the same way that quaternions can only represent rotations around the origin, for reflections, they can only represent reflections in planes which pass through the origin.
To reflect a point: make up a quaternion 'in', from the point, as follows:
in.w = 0
in.x = Pin.x
in.y = Pin.y
in.z = Pin.z
Then form a quaternion 'q' to represent the reflection, the real part is zero and the imaginary part represents the normal to the reflection plane (the direction which the points move).
q.w = 0
q.x = normal.x
q.y = normal.y
q.z = normal.z
We can then transform the point using the formula: Pout = q * Pin * q
example
to reflect point x=2,y=2,z=2 in plane x
so in = i2 + j2 + k2
and q = i
so putting these into the formula Pout = q * Pin * q we get:
Pout = i * (i2 + j2 + k2) * i
= i * (-2 + ji2 + ki2)
= i * (-2 - k2 + j2)
= -i2 - ik2 + ij2
= -i2 + j2 + k2
which is the expected result
Differences between using quaternions for rotations and reflections
| rotations | reflections | |
|---|---|---|
| transforming a point | Pout = q * Pin * conj(q) | Pout = q * Pin * q |
| combining tranforms | q1*q2 multiply to get a quaternion to represent a combination of two separate rotations. |
Cant combine reflections in this way. Combining two reflections gives a rotation, but we cant do it by simply multiplying the two quaternions. |
| real part | The real part depends on the amount of rotation. | The real part is zero. There is less information required for reflection, its either reflected or not. |
| normalising | q.w²+q.x²+q.y²+q.z²=1 if we want pure rotation without any expansion or contraction then the sum of the squares of all four elements equals unity. |
q.x²+q.y²+q.z²=1 since the real part is zero we only need to normalise the imaginary components. |
| inverse | conj(q) represents the inverse rotation to q | To invert a reflection just do it again. conj(q) represents the same reflection as q |
Full expansion of terms
If we fully expand the terms Pout = q * Pin * q
out.w=
( q.w*q.w -q.x*q.x -q.y*q.y -q.z*q.z)*in.w +( -2*q.w*q.x)*in.x +(
-2*q.w*q.y)*in.y +( -2*q.w*q.z)*in.z
out.x=
( 2*q.w*q.x)*in.w +( q.w*q.w -q.x*q.x +q.y*q.y +q.z*q.z)*in.x +(
-2*q.x*q.y)*in.y +( -2*q.x*q.z)*in.z
out.y=
( 2*q.w*q.y)*in.w +( -2*q.x*q.y)*in.x +( q.w*q.w +q.x*q.x -q.y*q.y
+q.z*q.z)*in.y +( -2*q.y*q.z)*in.z
out.z=
( 2*q.w*q.z)*in.w +( -2*q.x*q.z)*in.x +( -2*q.y*q.z)*in.y +( q.w*q.w
+q.x*q.x +q.y*q.y -q.z*q.z)*in.z
setting in.w and q.w to zero as explained above gives:
out.w=
0
out.x=
( -q.x*q.x +q.y*q.y +q.z*q.z)*in.x +( -2*q.x*q.y)*in.y +(
-2*q.x*q.z)*in.z
out.y=
( -2*q.x*q.y)*in.x +( q.x*q.x -q.y*q.y +q.z*q.z)*in.y +(
-2*q.y*q.z)*in.z
out.z=
( -2*q.x*q.z)*in.x +( -2*q.y*q.z)*in.y +( q.x*q.x +q.y*q.y
-q.z*q.z)*in.z
This is the same as the matrix above showing that the two methods are equivalent.
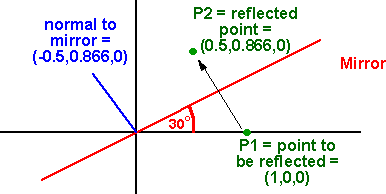
Example
As an example we want to reflect the point (1,0,0) in a plane at 30 degrees. P2 = q * P1 * q P2 = (0,-0.5 i , 0.866 j, 0 k) (1 i,0 j,0 k) (0,-0.5 i , 0.866 j, 0 k) P2 = - (0,-0.5 i , 0.866 j, 0 k) (0.5, 0.866 k) P2 = 0.5 i + 0.866 j |