For two dimensional rotations about x,y we can represent it with the following 3×3 matrix:
| r00 | r01 | x - r00*x - r01*y |
| r10 | r11 | y - r10*x - r11*y |
| 0 | 0 | 1 |
This represents the same as rotating round the origin but offset by:
(- r00*x - r01*y, - r10*x - r11*y).
For three dimensional rotations about x,y we can represent it with the following 4×4 matrix:
| r00 | r01 | r02 | x - r00*x - r01*y - r02*z |
| r10 | r11 | r12 | y - r10*x - r11*y - r12*z |
| r20 | r21 | r22 | z - r20*x - r21*y - r22*z |
| 0 | 0 | 0 | 1 |
This represents the same as rotating round the origin but offset by:
(- r00*x - r01*y - r02*z,- r10*x - r11*y - r12*z,- r20*x - r21*y - r22*z).
We will then go on to show that, in two dimensions, that the converse is also true. That is any combination of translation and rotation can be represented by a single rotation provided that we choose the correct point to rotate it around.
Combined Rotation and Translation
In order to calculate the rotation about any arbitrary point we need to calculate its new rotation and translation. In other words rotation about a point is an 'proper' isometry transformation' which means that it has a linear and a rotational component.
Assume we have a matrix [R0] which defines a rotation about the origin:
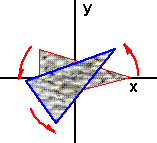
We now want to apply this same rotation but about an arbitrary point P:
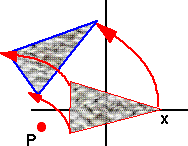
As we can see its orientation is the same as if it had been rotated about the origin, but it has been translated to a different point on space by the rotation.
In order to prove this and to calculate the amount of linear translation we need to replace:
- translate about arbitrary point P (Px,Py,Pz).
With the following 3 simpler transforms which, when done in order, are equivalent:
- translate the arbitrary point to the origin (subtract P which is translate by -Px,-Py,-Pz)
- rotate about the origin (can use 3×3 matrix R0)
- then translate back. (add P which is translate by +Px,+Py,+Pz)
So if we are using the global frame-of-reference (as explained here)
then,
[resulting transform] = [third transform] * [second transform] * [first transform]
[resulting transform] = [+Px,+Py,+Pz] * [rotation] * [-Px,-Py,-Pz]
Note for matrix algebra, the order of operations is important, so these translations do not cancel out.
So matrix representing rotation about a given point is:
[R] = [T]-1 * [R0] * [T]
where:
[T]-1 = inverse transform = translation of point to origin
| 1 | 0 | 0 | x |
| 0 | 1 | 0 | y |
| 0 | 0 | 1 | z |
| 0 | 0 | 0 | 1 |
[R0] = rotation about origin (if this is not clear see this discussion)
| r00 | r01 | r02 | 0 |
| r10 | r11 | r12 | 0 |
| r20 | r21 | r22 | 0 |
| 0 | 0 | 0 | 1 |
[T] = translation of origin to point
| 1 | 0 | 0 | -x |
| 0 | 1 | 0 | -y |
| 0 | 0 | 1 | -z |
| 0 | 0 | 0 | 1 |
When these matrices are multiplied this will give the following result for rotation about x,y,z:
(to see all the steps see this page)
| r00 | r01 | r02 | x - r00*x - r01*y - r02*z |
| r10 | r11 | r12 | y - r10*x - r11*y - r12*z |
| r20 | r21 | r22 | z - r20*x - r21*y - r22*z |
| 0 | 0 | 0 | 1 |
So the rotational components are the same but the rotation moves the position of the centre.
Isometry in 2 dimensions SE(2)
We now want to test the converse, that is, any combination of translation and rotation can be represented by a single rotation provided that we choose the correct point to rotate it around.
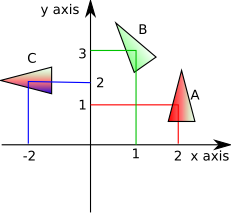
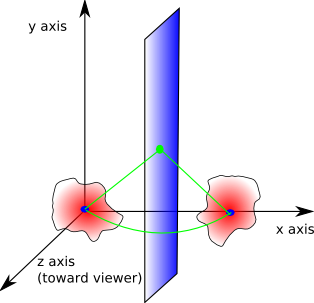
Imagine that we want to transform the solid body at 'A' into the solid body at 'B'
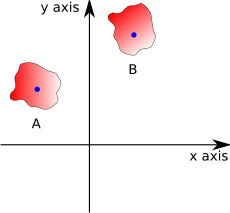
Then we can define a point on A (such as the centre-of-mass) and the corresponding point on B. We can then combine two transforms:
- Do a linear translation such that the point on 'A' is transformed to the point on 'B'.
- Do a rotation about the point so that the solid body is correctly transformed.
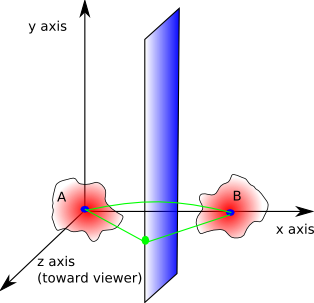
However, there is a second option, we can do the translation all in one rotation:
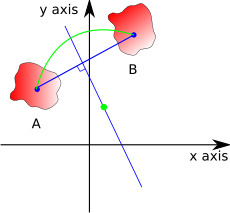
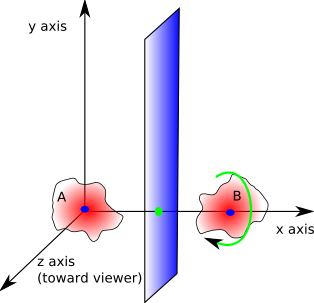
So, provided that we can find a suitable point to rotate around (in the above example shown as green point) we can do the translation and rotation in one operation. The point that we rotate around must by equidistant to the chosen point on each body, therefore it must lie on a line perpendicular to the line joining the two points. So is there always a point that we can find that will do any combination of translation and rotation? To find out we can take two extremes:
- If the rotation point is exactly in the middle of the two objects then the object will be rotated by 180 degrees.
- If the rotating point is at infinity along the bisecting line then the object is translated only and the rotation will be zero.
By putting the point at some distance between these we can get any rotation between 0 and 180 degrees. We can get negative angles by moving in the opposite direction along the line.
Therefore we can do any rotation, translation combination in one rotation.
Doing the rotation-translation in one operation like this can make some calculations simpler and we don't have to consider whether we do the rotation around its original position first and then the translation, or do the translation first and then the rotation about its final position, or do a translation to the mid point first, then the rotation about the mid position and then the final half translation.
Calculating Rotation Point
Given a translation (specified by a 2D vector) and a rotation (specified by a scalar angle in radians) how do we calculate the rotation point P ?
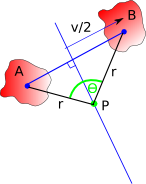
We know the points A and B and the angle at P which is theta.
sin(θ/2) = v/(2*r)
r = v/(2*sin(θ/2))
where:
- r = scalar distance of P from both A and B
- v = scalar distance of B from A
- θ = angle of rotation
We also know by Pythagoras:
(Px - Ax)2 + (Py - Ay)2 = r2
(Px - Bx)2 + (Py - By)2 = r2
This is getting a bit messy! Can we solve for P in vector coordinates?
I think I will have to give up with this approach and instead invert the matrix equations that we started with:
From the matrix derived above:
| r00 | r01 | x - r00*x - r01*y |
| r10 | r11 | y - r10*x - r11*y |
| 0 | 0 | 1 |
we get equations for offset:
Offsetx = x - r00*x - r01*y
Offsety = y - r10*x - r11*y
Where:
- Offset = linear distance that a point on the object has moved.
- x, y = coordinates of the point we are rotating around (relative to initial position of object).
We want to solve for x and y so we take the inverse of:
|
= |
|
|
to give:
|
= |
|
|
|
In this case the rotation matrix is:
| cos(θ) | -sin(θ) |
| sin(θ) | cos(θ) |
where
θ = angle of rotation
which gives:
|
= |
|
|
|
expanding out the determinant (and using sin2(θ)+cos2(θ)=1) gives:
|
= |
|
|
|
Check
We can check some special cases to see if we are getting reasonable results:
if θ = 0 then:
|
= | ∞ |
|
|
If theta = 0 then the rotation point is at infinity.
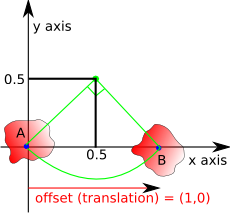
if θ = 90° then:
|
= |
|
|
|
so if the offset is at (1,0) then the rotation point is at (0.5,0.5)
if θ = 180° then:
|
= | 1/4 |
|
|
So we rotate around a point half way to B.
Combining Rotations about different Points
How do we apply two such rotations, one after the other, to produce a third rotation which is equivalent?
So imagine we apply a rotation of:
| ra00 | ra01 |
| ra10 | ra11 |
Centred at: (tax,tay,taz) followed by a rotation of:
| rb00 | rb01 |
| rb10 | rb11 |
Centred at: (tbx,tby,tbz)
The overall rotation is just the product of the two rotation matricies:
|
= |
|
|
The offset will be:
| tax - ra00*tax - ra01*tay + tbx - rb00*tbx - rb01*tby |
| tay - ra10*tax - ra11*tay + tbx - rb00*tbx - rb01*tby |
So the overall centre will be: