The fundamental homomorphism theorem states that. If φ: G->H is a homomorphism, then
Im(φ)
G / Ker(φ)
Example: D3 to C3
Lets look at a morphism from D3 to C3:
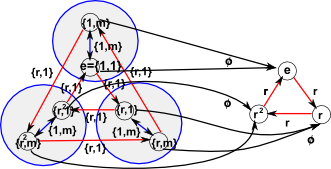
So, in this case,
- Im(φ) = 1,r,r²
- G = {1,1}, {r,1}, {r²,1},{1,m}, {r,m}, {r²,m}
- Ker(φ) = {1,1},{1,m}
So if we divide {1,1}, {r,1}, {r²,1},{1,m}, {r,m}, {r²,m} by {1,1},{1,m} we get
{1,N}, {r,N}, {r²,N}
where N stands for the larger circles in the diagram.
We can see that the group of big circles is isomorphic to C3 and so Im(φ)G / Ker(φ) as required.
Now lets look at a morphism, in the other direction, from C3 to D3:
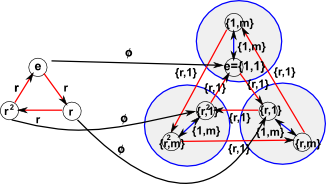
So, in this case,
- Im(φ) = {1,1}, {r,1}, {r²,1}
- G = 1,r,r²
- Ker(φ) = e
So this is relatively trivial as it is saying that 1,r,r² is isomorphic to {1,1}, {r,1}, {r²,1}
Futher Study
- normal subgroup
- short exact sequence
