The expression for:
(x + i y)n
where n is an integer.
is given by the following sum:
| (x + i y)n= |
|
|
(-i)k xn-k yk |
We can derive this from the binomial theorm:
| (a + b)n= |
|
|
(-1)k a n-k bk |
with 'a' replaced by x and 'b' replaced by iy
Square
We can look at a simplest we can take the case where n=2 which gives:
(x + i y)2
| z plane | w plane | |
|---|---|---|
 |
--> w=z² |
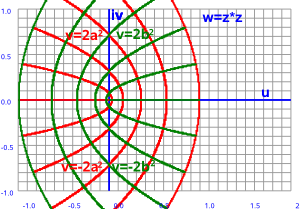 |
Pure real values always square to a positive value and pure imaginary values always square to a negative value. However real and imaginary parts together cover the whole plane.
Let the components of the input and output planes be:
z = x + i y and w = u + i v
lets take the example of the square function w = z²
so:
w = (x + i y)²
multiplying out gives:
w = x² - y² + i 2 x y
so the u and v components are:
u = x² - y²
v = 2 x y
Integer Powers
As shown above:
| (x + i y)n= |
|
|
(-i)k xn-k yk |
where:
| k | (-i)k | k! |
|---|---|---|
| 0 | 1 | 0 |
| 1 | -i | 1 |
| 2 | -1 | 2 |
| 3 | i | 6 |
| 4 | 1 | 24 |
So (-i)k cycles round every 4 entries, each step is a rotation by 90. The even values are real and the odd values are imaginary.
So the powers for n = 1 to 4 are:
| n | (x + i y)n | u | v |
|---|---|---|---|
| 1 | (x + i y)1 | x | y |
| 2 | (x + i y)2 | x²-y² | 2xy |
| 3 | (x + i y)3 | x3 - 3y²x | 3x²y -y3 |
| 4 | (x + i y)4 | x4 - 6x²y² - y4 | -2y3x-2yx3 |
