Maths - Complex Exponent

Euler's equation

r e^iθ = r (cos(θ) + i sin(θ))

For some reason, when I first came across this equation it came as a surprise to me and still my intuition makes me think there is some underling structure that I have missed. I think a lot of people have this reaction.

We were introduced to the exponential function and the trigometric functions (this page) separately as different examples of scalar functions. But now we are investigating complex functions we find that these two functions are related.

It is easy to prove Euler's equation, for example, by expanding both sides as a power series of complex numbers and comparing coefficients. Alternatively, you can solve the differential equation

df/dw =i*f

f(0)=1.

One solution is f =e^i*w and another is f=cos(w) + i*sin(w), so if you know that the solution is unique, then you get Euler's equation

(note: Euler's equation is not directly related to Euler angles its just that Euler was a prolific mathematician with a lot of things named after him).

Negative angles:

r e^-iθ = r (cos(θ) - i sin(θ))

Converse:

cos(z) = (e^iz + e^-iz)/2
sin(z) = (e^iz - e^-iz)/2

Polar Form

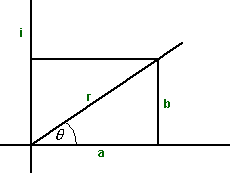
instead of a + i b the complex number could also be represented in what is known as the polar form:

r (cos(θ) + i sin(θ))

in other words replace:

• a = r cos(θ)
• b =r sin(θ)

we can use e^iθ = cos(θ) + i sin(θ) to give the exponential form:

r e^iθ

If we want combine the result of two rotations, for example rotate by θ1 then rotate by θ2, then we multiply the corresponding complex numbers because:

e^i(θ1+θ2) = e^iθ1 * e^iθ2

Or to combine two rotations by addition if we add the logarithms of the complex numbers.

Complex Functions

On this page we discussed how to represent and evaluate functions where the domain and codomain are complex numbers.

z plane		w plane
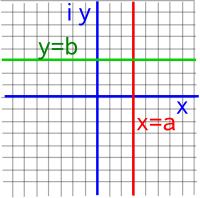	--> w=ez

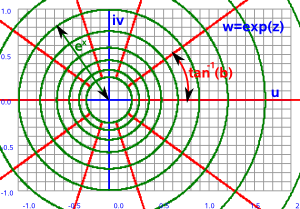Hyperbolic Functions

There is a hyperbolic equivalent of Euler's equation:

e^{D x} = cosh(x) + D sinh(x)
e^{-D x} = cosh(x) - D sinh(x)

This is similar to Euler's equation but applies to 'double numbers' (and similar algebra) rather than complex numbers.

Prerequisites

On this page we discussed how to represent and evaluate functions where the domain and codomain are complex numbers.

Elements of Equations