Maths - 3D multivector Functions

Prerequisites

To check the conventions and notation look at the following page first:

Reverse

The reverse function of a multivector reverses the order of its factors, including the order of the base values within a component. The reverse function is denoted by †, so the reversal of A is denoted by A†.

so for 3D vectors, if A = B† then:

a.e = b.e321 = -b.e123
a.e1 = b.e32 = -b.e23
a.e2 = b.e13 = -b.e31
a.e3 = b.e21 = -b.e12
a.e12 = b.e3
a.e31 = b.e2
a.e23 = b.e1
a.e123 = b.e

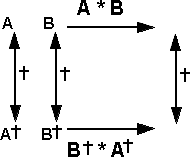
The reversal function is important for a number of reasons, one reason is that it can map a multiplication into another multiplication with the order of the multiplicands reversed:

(A * B)† = B†* A†

We can think of this as a morphism where † maps to an equivalent expression with order of multiplication reversed.

morphism

Another application for the reversal function is to specify a transformation from one vector field to another:

pout = A pin A†

In other words, if pin is a pure vector (i.e. real, bivector and tri-vector parts are all zero) then pout will also be a pure vector. I would appreciate any proof of this.If you have a proof, that I could add to this page, please let me know, In the 3D case I guess I could try the brute force approach of multiplying out the terms for a general expression A and p.

I think this may also apply to:

pout = A pin A -1

but not every multivector is invertible, one condition that should ensure that a multivector is invertible is:

A A† = scalar

If we apply this restriction to a multivector based on 3D vectors then we get the quaternion algebra as described here.

This reverses the order of the indexes, for general information about n-dimentional reverse see this page.

Ar
Ar† A A†
1 1 1
e1 e1 1
e2 e2 1
e3 e3 1
e12 e21 = -e12 1
e31 e13 = -e31 1
e23 e32 = -e23 1
e123 e321= -e123 1

Dual

This multiplies by e123 , for general information about n-dimentional dual see this page.

Ar
Ar* = e123 Ar
1 e123
e1 e123e1= -e32 = e23
e2 e123e2= -e13 = e31
e3 e123e3= e12
e12 e123e12= -e3
e31 e123e31= -e2
e23 e123e23= -e1
e123 e123e123= -1

Conjugate

The conjugate of Ar is denoted Ar~ where: Ar~*Ar = I = psudoscalar, for general information about n-dimentional conjugate see this page.

If Ar represents a transformation then Ar~ reverses the transformation

Ar
Ar~=(Ar†)* Ar~*Ar
1 (1)* = e123 e123
e1 (e1)* = e23 e123
e2 (e2)* = e31 e123
e3 (e3)* = e12 e123
e12 (-e12)* = e3 e123
e31 (-e31)* = e2 e123
e23 (-e23)* = e1 e123
e123 (-e123)* = 1 e123

The last column confirms that Ar~*Ar = I = psudoscalar.

Norm

under construction

Inverse

Can we use the same trick that we used with complex numbers, that is multiply top and bottom of equation by the conjugate, which will convert the denominator into a scalar making the division possible.

Terminology:

  input result (1/input)
scalar a.e e
vector a.e1 , a.e2 , a.e3 e1 , e2 , e3
bivector a.e12 , a.e31 , a.e23 e12 , e31 , e23
trivector a.e123 e123

Since I'm not yet sure how to calculate the inverse of a multivector, I'll first try an easier problem, how to calculate the inverse of parts of a multivector (scalar, vector, bivector and trivector).

inverse of scalar

e-1 = 1/a.e

inverse of vector

(e1 + e2 + e3 )-1

use conjugate (-e1 - e2 - e3 )

so multiplying a vector by its conjugate gives:

(e1 + e2 + e3 ) (-e1 -e2 -e3 ) = -e12 -e22 -e32

so (e1 + e2 + e3 )-1 = (-e1 - e2 - e3 )/(-e12 -e22 -e32)

e1 = a.e1/(a.e12 +a.e22 +a.e32)
e2 = a.e2/(a.e12 +a.e22 +a.e32)
e3 = a.e3/(a.e12 +a.e22 +a.e32)

inverse of bivector

(e12 + e31 + e23)-1

use conjugate (-e12 - e31 - e23)

so multiplying a bivector by its conjugate gives:

(e12 + e31 + e23) (-e12 - e31 - e23) = e122 + e312 + e232

so (e12 + e31 + e23)-1 = (-e12 - e31 - e23)/(e122 + e312 + e232)

e12 = - a.e12/(a.e12 +a.e22 +a.e32)
e31 = - a.e31/(a.e12 +a.e22 +a.e32)
e23 = - a.e23/(a.e12 +a.e22 +a.e32)

inverse of trivector

e123-1 = a.e123 / (a.e123 * a.e123) = -1/a.e123

inverse of multivector

If it follows the pattern then it would be:

(e1 + e2 + e3 + e12 + e31 + e23 + e123)-1 = (e -e1 -e2 -e3 - e12 - e31 - e23 + a.e123)/(e2 - ex2 - ey2 - ez2 + e122 + e312 + e232 - e1232)

but is it? this would make the conjugate e -e1 -e2 -e3 - e12 - e31 - e23 + a.e123

so if we multiply a multivector by this possible conjugate we get:

(a.e1 + a.e2 + a.e3 + a.e12 + a.e31 + a.e23 + a.e123)(a.e -a.e1 -a.e2 -a.e3 - a.e12 - a.e31 - a.e23 + a.e123)

which gives:

e = a.e2 - a.e12 - a.e22 - a.e32 + a.e122 + a.e312 + a.e232 - a.e1232
e123 = 2*a.e * a.e123 - 2*a.e1 *a.e23 -2*a.e2*a.e31 - 2*a.e3*a.e12

so due to this extra e123 term this will only work if:

a.e * a.e123 = a.e1 *a.e23 + a.e2*a.e31 + a.e3*a.e12

which would make the extra term zero.

Although not necessary to calculate the inverse, the calculation would be a lot simpler if:

1 = a.e2 - a.e12 - a.e22 - a.e32 + a.e122 + a.e312 + a.e232 - a.e1232

so if,

a.e * a.e123 = a.e1 *a.e23 + a.e2*a.e31 + a.e3*a.e12

and

1 = a.e2 - a.e12 - a.e22 - a.e32 + a.e122 + a.e312 + a.e232 - a.e1232

then,

(e1 + e2 + e3 + e12 + e31 + e23 + e123)-1 = e -e1 -e2 -e3 - e12 - e31 - e23 + a.e123

public final void invert(Matrix4d m1) {
m00 = m12*m23*m31 - m13*m22*m31 + m13*m21*m32 - m11*m23*m32 - m12*m21*m33 + m11*m22*m33;
m01 = m03*m22*m31 - m02*m23*m31 - m03*m21*m32 + m01*m23*m32 + m02*m21*m33 - m01*m22*m33;
m02 = m02*m13*m31 - m03*m12*m31 + m03*m11*m32 - m01*m13*m32 - m02*m11*m33 + m01*m12*m33;
m03 = m03*m12*m21 - m02*m13*m21 - m03*m11*m22 + m01*m13*m22 + m02*m11*m23 - m01*m12*m23;
m10 = m13*m22*m30 - m12*m23*m30 - m13*m20*m32 + m10*m23*m32 + m12*m20*m33 - m10*m22*m33;
m11 = m02*m23*m30 - m03*m22*m30 + m03*m20*m32 - m00*m23*m32 - m02*m20*m33 + m00*m22*m33;
m12 = m03*m12*m30 - m02*m13*m30 - m03*m10*m32 + m00*m13*m32 + m02*m10*m33 - m00*m12*m33;
m13 = m02*m13*m20 - m03*m12*m20 + m03*m10*m22 - m00*m13*m22 - m02*m10*m23 + m00*m12*m23;
m20 = m11*m23*m30 - m13*m21*m30 + m13*m20*m31 - m10*m23*m31 - m11*m20*m33 + m10*m21*m33;
m21 = m03*m21*m30 - m01*m23*m30 - m03*m20*m31 + m00*m23*m31 + m01*m20*m33 - m00*m21*m33;
m22 = m01*m13*m30 - m03*m11*m30 + m03*m10*m31 - m00*m13*m31 - m01*m10*m33 + m00*m11*m33;
m23 = m03*m11*m20 - m01*m13*m20 - m03*m10*m21 + m00*m13*m21 + m01*m10*m23 - m00*m11*m23;
m30 = m12*m21*m30 - m11*m22*m30 - m12*m20*m31 + m10*m22*m31 + m11*m20*m32 - m10*m21*m32;
m31 = m01*m22*m30 - m02*m21*m30 + m02*m20*m31 - m00*m22*m31 - m01*m20*m32 + m00*m21*m32;
m32 = m02*m11*m30 - m01*m12*m30 - m02*m10*m31 + m00*m12*m31 + m01*m10*m32 - m00*m11*m32;
m33 = m01*m12*m20 - m02*m11*m20 + m02*m10*m21 - m00*m12*m21 - m01*m10*m22 + m00*m11*m22;
scale(1/m1.determinant());
}

 

Exponential

We define the exponential of multivector a as ea º åi=0¥ ai / i ! .
In particular:
ea is the traditional scalar exponential function
For any pure square multivector [ a2 = ±|a|2 ] we have ea = cos|a| + a~ sin|a| if a2 < 0 ;
cosh|a| + a~ sinh|a| if a2 > 0 ;
1+a if a2 = 0.

For unit multivector a:
eafeay = ea(f+y)
(d/df) elaf =lea(lf+p/2) =laelaf

Involution

a# = sum k=0(N (-1)k a <k> = a<+> - a<-> .

Determinant

The determinant of a multivector can be calculated from the table shown for the multipication of each dimentional vectors.

determinant = m11 m22 m33 + m12 m23 m31 + m13 m21 m32 - m11 m23 m32 - m12 m 21 m33 - m13 m22 m31

metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.
flag flag flag flag flag flag Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics (Fundamental Theories of Physics). This book is intended for mathematicians and physicists rather than programmers, it is very theoretical. It covers the algebra and calculus of multivectors of any dimension and is not specific to 3D modelling.

 

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.