| Initial and Final algebras have nice mathematical properties, for instance, initial algebras can be built up from other initial algebras. So, in the case of DAMGs, we can recursively compose larger graphs from smaller graphs. Graphs, in general, are not initial because they require labeled sets. However there is a form of graph which is initial, we call this Directed Acyclic Multi Graph (DAMG), this graph: |
- Is directed (edges have direction arrows).
- There may be more than one edge between a given pair of vertices (hence multigraph)
- Incoming and outgoing edges of a vertex are ordered.
- The graph, as a whole, may have inputs and outputs (that is an edge may not have a vertex at the end of it). DAMGs don't necessarily have to have inputs and outputs but, when present, they allow graphs to plug-in to other graphs.
I have used a lot of the information about this algebra from this paper: [Jeremy Gibbons - An Initial−Algebra Approach to Directed Acyclic Graphs]
This algebra is a 'symmetric strict monoidal' category.
| So inside the DAMG we can have any graph which meets the above requirements (no loops and so on). Externally it has a number of inputs and outputs. We usually draw the inputs on the left and outputs on the right. |
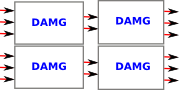 |
What gives them nice mathematical properties is that we can link them together, both vertically and horizontally. |
| If the DAMG structures were always aligned in a strict array, as above, then the bottom part of the overall structure could not interact with the top. However there is no requirement for each column to align and therefore we can get as much interaction as required by combining in the appropriate way. | 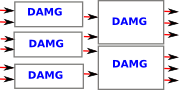 |
Constructors
We can construct any DAMG from 6 constructor types (basic building blocks):
Vertex(S,m,n)
 |
A vertex in the graph. If defined over some set 'S' then the vertex can be associated with an element of that set. 'm' and 'n' are NNIs which represent the number of input and output edges. The inputs are usually shown on the left of the vertex and the outputs on the right, so the flow is usually drawn as going from left to right. |
Edge
This represents an edge going from left to right. Not every edge on the graph will have an explicit edge term, often an output from a vertex will be plugged directly into the input of another vertex. An explicit edge is only needed as a sort of spacer to travel across a column without interacting.
Beside
This links up two sections of graph top to bottom.
Before
This links up two sections of graph left to right.
Empty
The empty graph. This has a similar function to say 'zero' for natural numbers.
Swap
 |
This swaps over a set of edges to allow edges to move up and down so that they can plug onto different vertices. |
Axioms
| Beside is associative | DamgBeside(x,DamgBeside(y,z)) = DamgBeside(DamgBeside(x,y),z) |
| Before is associative | DamgBefore(x,DamgBefore(y,z)) = DamgBefore(DamgBefore(x,y),z) |
| Unit of graph is Empty | 0 × x = Empty() |
| The number of output edges must match the number of input edges following | DamgBefore(DamgVertex(S,a,b),DamgVertex(S,c,d)) b=c |
abiding law When we combine 'beside' and 'before' then we can somtimes change which is outer and which is inner providing dimensions work out. |
DamgBeside(DamgBefore(DamgVertex(S,a,b),DamgVertex(S,a,a)), DamgBefore(DamgVertex(S,a,b),DamgVertex(S,a,a))) = DamgBefore(DamgBeside(DamgVertex(S,a,b),DamgVertex(S,a,a)), DamgBeside(DamgVertex(S,a,b),DamgVertex(S,a,a)))
|
| Swapping zero connections makes no difference | DamgSwap(m,0) = m × DamgEdge() |
| Swapping n connections and then p connections is equivelent to swapping n+p connections |  |
| Special case of swap law | DamgBefore(DamgSwap(m,n),DamgSwap(n,m)) = (m+n) × DamgEdge()
swap(n,m) cancells out swap(m,n) |
| Another special case of swap law using edges |  |
Example
Here we can see how 'vertex', 'edge' and 'swap' form components. 'beside and 'before' define how they fit together:
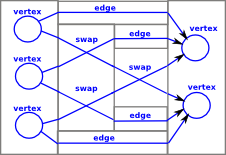 |
I compiled the FriCAS code below and then entered the above graph as follows:
(1) -> D:=Damg(String)
(1) Damg(String)
Type: Type
(2) -> x:=DamgBefore(DamgBefore(DamgBeside(DamgBeside(DamgVertex("v1",0,2),
DamgVertex("v2",0,2)),DamgVertex("v2",0,2)),DamgBeside(DamgBeside(DamgEdge()$D,
DamgBefore(DamgBeside(DamgSwap(1,1)$D,DamgSwap(1,1)$D),
DamgBeside(DamgBeside(DamgEdge()$D,DamgSwap(1,1)$D),
DamgEdge()$D))),DamgEdge()$D)),DamgBeside(DamgVertex("v1",3,0),
DamgVertex("v2",3,0)))
(2)
"before(before(beside(beside(vertex(0,2)vertex(0,2))vertex(0,2))beside(beside
(edge(before(beside(swap(1,1)swap(1,1))beside(beside(edge(swap(1,1))edge()))e
dge())beside(vertex(3,0)vertex(3,0)))"
Type: Damg(String)
(3) -> |
Well this constructs the structure but its horrible, it does not give any intuitive feel for the graph structure. I think the problem is not really FriCAS, any program which uses the command line interface would struggle to represent this type of structure. I think it really needs a more graphical interface.
Code
The following is just boilerplate code to construct and deconstruct a DAMG. It would be nice if SPAD had a way to automatically generate such boilerplate code for initial and final algebras.
To make this more useful we need code to convert this into other graph types and to produce graphical output.
)abbrev domain DAMG Damg
++ Author: Martin Baker
++ Date Created: May 2013
++ Date Last Updated: May 2013
++ Basic Operations:
++ Related Constructors:
++ Keywords: graph theory
++ Description: an initial graph similar to a DAG without the need for
++ labeled sets
++
++ References:
++ http: //www.euclideanspace.com/maths/standards/program/mycode/discrete/graph/
Damg(S) : Exports == Implementation where
S : SetCategory
Exports ==> Join(CoercibleTo(OutputForm), SetCategory) with
-- constructors
DamgVertex : (ob:S,m1:NonNegativeInteger,n1:NonNegativeInteger) -> %
++ Vertex constructor
DamgEdge : () -> %
++ Edge constructor
DamgBeside : (a:%,b:%) -> %
++ Beside constructor
DamgBefore : (a:%,b:%) -> %
++ Before constructor
DamgEmpty : () -> %
++ Empty constructor
DamgSwap : (m:NonNegativeInteger,n:NonNegativeInteger) -> %
++ Swap constructor
-- destructors, this is not necessarily a final algebra but we still need
-- to be able to get at the components of instances.
isVertex? : (n : %) -> Boolean
++ introspection: returns true if this is a Vertex
isEdge? : (n : %) -> Boolean
++ introspection: returns true if this is a Edge
isBeside? : (n : %) -> Boolean
++ introspection: returns true if this is a Beside
isBefore? : (n : %) -> Boolean
++ introspection: returns true if this is a Before
isEmpty? : (n : %) -> Boolean
++ introspection: returns true if this is Empty
isSwap? : (n : %) -> Boolean
++ introspection: returns true if this is a Swap
getIntValues : (n : %) -> List NonNegativeInteger
++ if term has integers then get them.
getChildren : (n : %) -> List %
++ if term has child nodes then get them.
Implementation ==> add
Rep := Union(_
vertex: Record(v:S,m:NonNegativeInteger,n:NonNegativeInteger),_
edge : Boolean,_
beside : Record(a:%,b:%),_
before : Record(a:%,b:%,c:Boolean),_
empty : Record(m:NonNegativeInteger),_
swap : Record(m:NonNegativeInteger,n:NonNegativeInteger))
-- Since this domain is initial the terms of the representation
-- can correspond exactly to the constructors.
-- Vertex constructor
DamgVertex(ob:S,m1:NonNegativeInteger,n1:NonNegativeInteger) : % ==
[[ob,m1,n1]]
-- Edge constructor
DamgEdge() : % == [true]
-- Beside constructor
DamgBeside(a1:%,b1:%) : % == [[a1,b1]]
-- Before constructor
DamgBefore(a1:%,b1:%) : % == [[a1,b1,true]]
-- Empty constructor
DamgEmpty() : % == [[0::NonNegativeInteger]]
-- Swap constructor
DamgSwap(m1:NonNegativeInteger,n1:NonNegativeInteger) : % == [[m1,n1]]
-- introspection: returns true if this is a Vertex
isVertex?(n1 : %):Boolean ==
(n1 case vertex)
-- introspection: returns true if this is a Edge
isEdge?(n1 : %):Boolean ==
(n1 case edge)
-- introspection: returns true if this is a Beside
isBeside?(n1 : %):Boolean ==
(n1 case beside)
-- introspection: returns true if this is a Before
isBefore?(n1 : %):Boolean ==
(n1 case before)
-- introspection: returns true if this is Empty
isEmpty?(n1 : %):Boolean ==
(n1 case empty)
-- introspection: returns true if this is a Swap
isSwap?(n1 : %):Boolean ==
(n1 case swap)
-- if term has integers then get them.
getIntValues(n1 : %):List NonNegativeInteger ==
if isVertex?(n1) then return [n1.vertex.m, n1.vertex.n]
if isSwap?(n1) then return [n1.swap.m, n1.swap.n]
[]
-- if term has child nodes then get them.
getChildren(n1 : %):List % ==
if isBeside?(n1) then return [n1.beside.a, n1.beside.b]
if isBefore?(n1) then return [n1.before.a, n1.before.b]
[]
-- return string representation using deBruijn index for
-- bound variables.
-- notation assumes association to the left, in the absence of
-- brackets, the term to the left binds more tightly than the
-- one on the right.
toString(n1 : %) : String ==
s:String := ""
if isVertex?(n1) then
s := concat(["vertex(",string(getIntValues(n1).1),_
",",string(getIntValues(n1).2),_
")"])@String
if isEdge?(n1) then
s := "edge("
if isBeside?(n1) then
s := concat(["beside(",toString(getChildren(n1).1),_
toString(getChildren(n1).2),")"])@String
if isBefore?(n1) then
s := concat(["before(",toString(getChildren(n1).1),_
toString(getChildren(n1).2),")"])@String
if isEmpty?(n1) then
s := "empty"
if isSwap?(n1) then
s := concat(["swap(",string(getIntValues(n1).1),_
",",string(getIntValues(n1).2),_
")"])@String
s
-- output
coerce(n : %) : OutputForm ==
toString(n)::OutputForm
@ |

