Here we take an intuitive and non-rigorous look at multidimensional functions, the requirements to do calculus and avoiding singularities.
On this page we looked at functions of a complex variable and we found that a useful technique for analysing functions is to plot what happens to vertical and horizontal lines:
| z plane | w plane | |
|---|---|---|
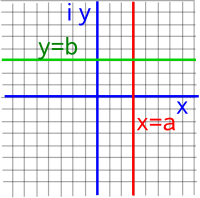 |
--> w=z² |
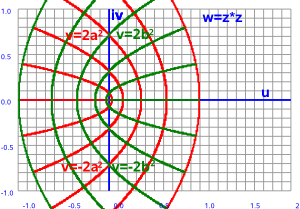 |
When we applied calculus ideas to this on this page we found that in order to differentiate and integrate then the function needs to have the following properties:
- Conformal - angles are preserved so since the input vertical and horizontal lines are at 90° to each other then the output must also be at 90°.
- Analytic - squares map to squares.
So, in order to investigate the properties of a well behaved differential function, we will start with a flat plane and then see the effects of introducing distortions.
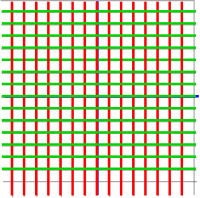
Lets start by pushing apart the vertical lines:
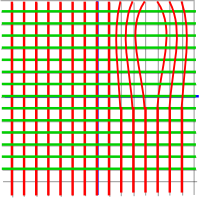
However now the red and green lines no longer cross at right angles so we need to move the green lines in to compensate:
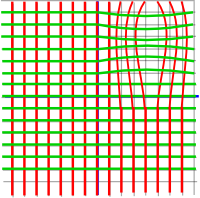
Now the lines cross each other at right angles but this his has the effect of elongating the squares into rectangles (no matter how infinitesimally small we make the squares) and so this function wont be analytic.
Interestingly the squares appear to transform to rectangles which have the same area as the original square. However conservation of area is not a requirement, retention of the square shape is, so this does not appear to work.
So its not as easy as first thought to meet the requirements for a differentiable function. We will need to try a different approach:

This doesn't quite work either (I suspect there is not a way to mix linear and non linear functions in this way). However in some respects this is much closer to what we want, infinitesimally squares will be mapped to something much closer to squares, so I think this is as close as we are going to get with this approach.
It seems that making the transformation more square has been done at the cost of introducing a singularity at the centre of the place where we introduced the distortion. We can also see that all the functions of a complex variable that we looked at on this page also have a singularity so it appears that it is not possible to make complex functions differentiable at all places, the best we can do is to group the problem areas together into one or more points known as singularities.
However there is a way round this and that is to map the output of our function to a higher dimensional space our output forming a subset of this higher dimensional space (such as a 2 dimensional surface in 3 dimensions).

Now with an extra dimension we can allow the size of individual squares to increase and even the average size of a given subarea can increase without squashing the area around it.
Also we don't need to introduce any singularities.
It would be nice to make this more rigorous, for instance it would be good to be able to work out:
- How many dimensions are required to make a given function differentiable?
- Can we always get rid of singularities by adding dimensions?

