We can relate type theory to category theory by linking:
- types to objects
- terms to arrows
| So if a category has various objects each of these could be related to a type. | 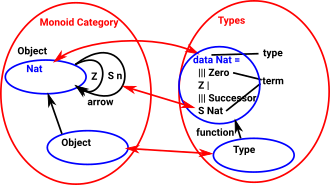 |
Example of Set
How could a set type be related to a set category?
In the diagram below each object is a set of a given size.
| This diagram doesn't yet reflect the nature of set since set category can have an arrow from every set to every other set except empty set. |  |
In order to construct Nat or Vect above we need to call multiple constructors for each instance, for example, to constuct '2' we need to call Z and S and S. So is this a single instance of a type or 3 instances?
Category Theory, Logic and Type Theory
| Category Theory | Logic | Type Theory |
|---|---|---|
| object say A, B ... | type | |
| arrow say m:A->B | relation proved term |
inhabited term |
| idA | reflexitiviy | |
| given m:A->B and n:B->C there is n•m:A->C | ||
| given e:E->A then idA•e=e and given m:A->B then m•idA=m |
||
| given m:A->B and n:B->C and l:C->D then l•(n•m)=(l•n)•m |
Cartesian Closed Category (CCC)
In category theory the locally closed Cartesian category is the counterpart of extensional type theory. For intensional type theory we need to add quotient completions - used for modeling extensional type theories into intensional ones. |
 |
see W-types
The category C is called Cartesian closed if and only if it satisfies the following three properties:
- It has a terminal object.
- Any two objects X and Y of C have a product X ×Y in C.
- Any two objects Y and Z of C have an exponential ZY in C.
Examples specially relevant to type theory:
- In order theory, complete partial orders (cpos) have a natural topology, the Scott topology, whose continuous maps do form a Cartesian closed category (that is, the objects are the cpos, and the morphisms are the Scott continuous maps).
- A Heyting algebra is a Cartesian closed (bounded) lattice. An important example arises from topological spaces. If X is a topological space, then the open sets in X form the objects of a category O(X) for which there is a unique morphism from U to V if U is a subset of V and no morphism otherwise. This poset is a Cartesian closed category: the "product" of U and V is the intersection of U and V and the exponential UV is the interior of U∪(X\V).
- The category of simplicial sets (which are functors X : Δop -> Set) is Cartesian closed.