NBG is a rigorous axomatic foundation for set theory based on work by: John von Neuman, Paul Bernays and Kurt Gödel. It is one of many intended to eliminate potential paradoxes, in set theory, pointed out by Bertrand Russel (also see ZF).
| The NBG axiomatic formulation makes a distinction between 'sets' and 'classes'. All entities in NBG are classes, the word 'set' is reserved for collections that are members of other classes. |  |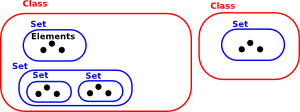
So the outermost 'class' is not a 'set', this is known as a 'proper class'.
The Comprehension Principle is modified by requiring the objects referred to are sets.
Axioms
If A and B are classes and C and D are sets:
- The axiom of Extension: Classes are equal if and only if they have the same members. For all c
A, if and only if cB then A=B. - The axiom of empty set: There exists a set C such that for all x, it is false that xC.
- The axiom of Class Comprehension: For any formula φ which does not quantify over classes, there is a class A such that xA if and only if φ(x) is true.
- The Axiom of Pairing: For any two sets C and D, there is a set with exactly C and D as members.
- The Axiom of size: For any class A, there is a set c such that c=Rep(A) if and only if there is no total one-to-one function between A and the class of all sets. This is the one that creates that definition of classes as things too big to be sets.
- The Axiom of union: for any set x, there is a set containing the members of the members of x. In other words, you can take the union of any set of sets.
- The Axiom of powerset: For any set x, there is a set which contains all of the subsets of x.
- The Axiom of infinity: There exists a set N where: * The empty set ∅ is a member of N; and * for each member x∈N, (x∪{x})∈N
- The Axiom of Foundation: All non-empty classes are disjoint from at least one of their elements.
- The Axiom of regularity: All non-empty sets are disjoint from at least one of their elements.
