Prerequisites
If you are not familiar with mathematical functions you may like to look at the following pages first:
Calculus
A mathematical function such as y=f(x) defines a value of y for every x.
Differentiation and Integration defines a whole function for a a given input function.
Differentiation
Differentiation defines the rate of change of a given function for every point on that function:
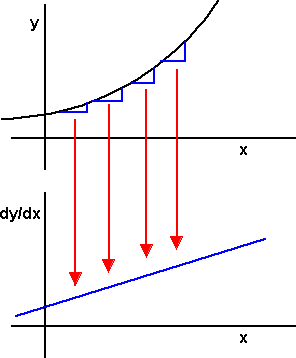
How this is done is explained on this page.
Integration
Integration defines the cumulative area under a given function for every point on that function:
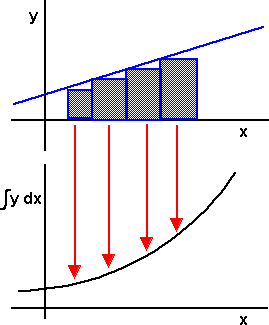
How this is done is explained on this page.
Leibnitz Notation
The Differential of a function f(x) is denoted by d f(x)/dx.
Even if you don't want to learn any more about calculus it is useful to recognise that:
d f(x)/dx means the rate of change of f(x) with respect to x. To take a more specific example:
d distance / d time
Means the rate of change of distance with respect to time, in other words, as time changes what is the corresponding change in distance. In other words the value of velocity for every value of time.
So you will often see on this site, the form d ... / d ... means the rate of change of something with respect to something else.
Note: d f(x) does not mean d times f(x), instead d is an 'operator' acting on f(x). I guess that 'd' stands for difference.
Further Topics
For further explanation and derivation see this page.
So far we have been talking about scalar functions but we can also do calculus on other algebras such as:


