Maths - Changing Coordinates

An important topic for tensors is the way that they are affected by a change in coordinates. Also can we formulate our tensor equations in such a way that they are independent of the chosen coordinate system?

First we will start with a coordinate system based on a linear combination of orthogonal basis vectors.

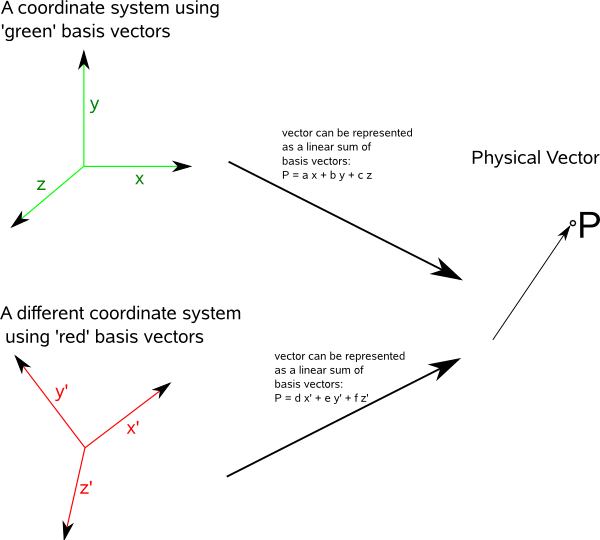
The physical vector 'p' can be represented by either:

p = ∑ v_ieⁱ in the red coordinate system and

p = ∑ v'_ie'ⁱ in the green coordinate system.

where:

• p = physical vector being represented in tensor terms
• v_i = tensor in the red coordinate system
• eⁱ= basis in the red coordinate system
• v'_i= tensor in the green coordinate system
• e'ⁱ = basis in the green coordinate system

So we can transform between the two using:

∑ v'^k = t^k_i v ⁱ

or

∑ e^k = t^'k_i e'ⁱ

where:

• t = a matrix tensor which rotates the vector v to vector '
• t' = a matrix tensor which rotates the basis e to the basis e'

Orthogonal Coordinates

We are considering the situation where a vector is measured as a linear combination of a number of basis vectors. We now add an additional condition that the basis vectors are mutually at 90° to each other. In this case we have:

e_i • e_j = δ_ij

where:

• e_i = a unit length basis vector
• e_j = another unit length basis vector perpendicular to the first.
• δ_ij= Kronecker Delta as described here.

If we choose a different set of basis vectors, but still perpendicular to each other, say e'_i and e'_j then we have:

e'_i • e'_j = δ_ij

To add more dimensions we can use:

e_ki • e_kj = δ_ij

This is derived from the above expression using the substitution property of the Kronecker Delta.

We could express the above in matrix notation:

a^T a = [I]

where:

• a = a vector
• a^T= transpose of 'a'
• [I] = the identity matrix

We can combine these terminologies to give:

(a^T a)_ij = e_ki • e_kj = δ_ij

Any of these equations defines an orthogonal transformation.

Curvilinear Coordinate Systems

The simplest case contravarient and covarient tensors is to look at contravarient and covarient vectors. These

• The different ways that they vary with a change in coordinates shown by the partial differentials below.
• As duals of each other - for example in 3D vectors and bivectors are duals.
• Represented as column or row vectors.

For a discussion about measuring the curvature of space, see this page.

Dyads

The tensor product of two vectors e_i and e_j may be denoted by e_i e_j or the operation may be shown explicitly by e_i e_j

A tensor can then be represented as:

∑ a_ij e_i e_j

 

EuclideanSpace

home

Coordinate Systems

Duality

Hyperbola