We can apply translation by using vector addition:
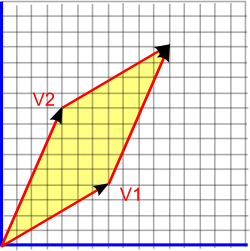
but it would be useful if we could do this using multiplication, then we could use the same operation for both translation and rotation.
One way to convert between addition and multiplication operations is to use the exponential operation (inverse of log).
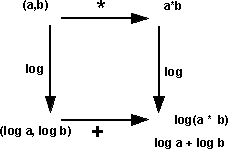
Double Number Exponent
In order to calculate a transform in 2 dimensional euclidean space (that is 2 'space' dimensions which square to positive) then we need to work using double numbers (sometimes known as split complex numbers) that is an algebra which is like complex numbers but where i²=+1 (except we denote i as D).
This seems reasonable, since we are working in a space where both dimensions square to +ve, it make sense to use an algebra where both dimensions square to +ve.
To calculate the exponent of a double number we can use the hyperbolic version of Euler's equation which gives:
w = ex(cosh(y) + D sinh(y))
as discussed here.
| Double Exponent | 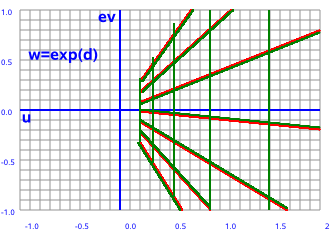 |
|---|
Two Dimensional Minkowski Space
If instead of 2D Euclidean space we are working in a space where one dimension squares to +ve and the other to -ve (one space dimension and one time dimension) then we can use exactly the same calculations except that we do the calculations using complex numbers.
| Complex Exponent | 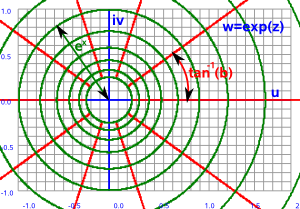 |
|---|
This means that in 2D Minkowski space translations have the same properties as rotations in 2D Euclidean space and in 2D Minkowski space rotations have the same properties as translations in 2D Euclidean space.
Double Number Exponent Calculator
The following calculator allows us to add two vectors by multiplying two double numbers, to do this:
- Enter the two vectors in x and y values (top left)
- Press both of the 'exp ->' buttons to calculate the exponents of both vectors.
- Press '*' button to multiply these values.
- Press '<- ln' button
- The resulting double number should be the vector sum of the double numbers above.
