Haskell

Values and Types

A value may be represented with its type signature, by using the :: symbol, or its type may be automatically inferred.

Haskell has strong, static typing.

Defining Functions

A function, in this case 'inc' may have a type signature and a definition:

Functions can only be defined in a limited way from console, using 'let' keyword. For more complicated fuctions it is necessay to put in a file.

Anonymous Functions

For the mathematical principles of lambda calculus see this page.

Prelude> (\x -> x*x) 3
9
Prelude> 

The \ character is intended to represent the λ symbol.

Defining Data

Types defined in prelude (effectivly built in types):

User Types

The 'data' keyword allows us to define a type constructor with its corresponding data constructors.

An algebraic user type uses a '|' symbol to provide alternative value constructors. This can be read as 'or'. It provides an equivalent of enumeration in other languages.

type synonyms

We can use an alternative name for a type by using the 'type' keyword. This is purely to make the code more readable.

type myID = Int
type String = [char]

newtype

This creates a new type from an existing type, it is like renaming an existing type, it hides this derivation and gives the type a new identity.

Variables

Variables in Haskell, and other pure functional languages, work differently than variables in imperative languages. A pure functional language can't have a state so a variable cant actually vary, we can assign, say x, a value:

Prelude> let x = 1
Prelude> x
1
Prelude> let x = 2
Prelude> x
2
Prelude> let x = x + 1
Prelude> x
^CInterrupted.
Prelude> 

Typeclasses

Haskell classes support polymorphism, overloading and inheritance, a class defines which operations can work on which inputs.

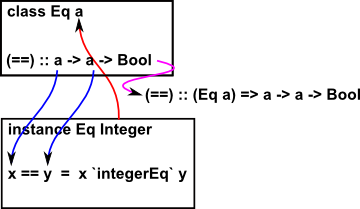
Haskell classes are not objects, in that they do not have data, as that would be state information which is not allowed in a pure functional program.

class MyCompare a where
    myEq,myNotEq :: a -> a -> Bool
    myEq x y = not (myNotEq x y)

defining an instance of a class:

instance MyCompare Int where
    myEq x y = x==y

In order to test this out I have put the following into a file:

class MyCompare a where
    myEq,myNotEq :: a -> a -> Bool
    myEq x y = not (myNotEq x y)

instance MyCompare Int where
    myEq x y = x==y
    myNotEq x y = x/=y

then load the file and get information about it:

*Main> :load mycompare.hs
[1 of 1] Compiling Main          ( mycompare.hs, interpreted )
Ok, modules loaded: Main.
*Main> :info myEq
class MyCompare a where
  myEq :: a -> a -> Bool
  ...
        -- Defined at mycompare.hs:2:4-7
*Main> :type myEq
myEq :: (MyCompare a) => a -> a -> Bool
*Main>

note that (MyCompare a) => means: for all types 'a' provided that 'a' is an instance of MyCompare.

Lists & Tuples

Lists

List values are represented by enclosing the values in square brackets seperated by commas:

['a','b','c']

List type also represented by putting in square brackets:

[Char]

In the following constructs the element 'a' is of polymorphic type. That is, lists can be defined of any other types.

This construct ':' appends to a list.

List Comprehensions

Arithmetic Sequence

Tuples

Pattern Matching

Pattern matching when calling functions:

addList (x:xs) = x + addList xs
addList [] = 0

'_' can be used as a wild card.

We can also pattern match on a algebraic value constructor.

Monads

see this page.

EuclideanSpace

home

Prerequisites

For information about how to install on openSUSE see this page.

For the mathematical principles of lambda calculus see this page.

Functional Programming and Category Theory

Endofunction