By: nobody ( Nobody/Anonymous )
Greetings, nice site!
2002-12-19 16:43
Hi Martin, et. al.,
Great stuff!
Another great resource, although I'm sure you've all come across it, are the articles by Chris Hecker :
http://www.d6.com/users/checker/dynamics.htm
Where, in the last article of his series, he goes on to derive a general formula for rigid body collision response, using an impulse method, much as in "Physics for Game Developers".
I'm getting into this whole area myself, time permitting, though there are plenty of heavy-duty distractions on the way! Ages ago though I wrote some applets for simulating collisions in 2D, e.g. http://www.rileys.demon.co.uk/HardBody.html, but my endeavours into 3D has thus far been limited to simple things, OPENGL and the theoretical side, the latter of which take some working through!
Regards
By: martinbaker ( Martin Baker )
RE: Greetings, nice site!
2002-12-21 08:56
Thanks,
Yes your right, I think its about time I revisited Chris Heckers articles, I looked at them when I first started this 3D programming, but at the time I was not able to fill in the gaps or complete the working to derive the equations for the collision response from the impulse equation that he gives (or did I miss it?). I think I’ve learned a bit since then so I’ll have another look. I don’t want to copy too much though in case I infringe his copyright.
I hope your work with 3D goes well, let me know if there is any scope for collaboration with what I’m doing.
Martin
By: nobody ( Nobody/Anonymous )
RE: Greetings, nice site!
2002-12-21 17:06
Hi Martin,
I think Chris Heckers' articles need to be printed and read multiple times, but are the best source of info on this area that I've come across from book or web (barring your site when it's finished of course :), and he gives loads of references, most of which I've not yet followed up. Incidentally MIT is putting its course material on the web. Fancy attending a linear algebra video lecture : http://ocw.mit.edu/18/18.06/f02/video-lectures/index.html :) They are very good.
Hecker derived the response equations for 2D and 3D, the equations including rotation and friction, although rushed a little at the end if I recall; his result also ties in with what I came up with, before I had seen an impulse approach, although in a different form. I just used the basic conservation laws, a little (heck, I did it lots of ways) like I shall show below for 1D but it's all the same in the end. Using impulse seems tidier and less work however.
On one of your web pages, you appear to be working on 1D collisions, I can show one method of solving this, although it looks terrible in ASCII.
Variable names to be used:
Object one:
m = mass
v = velocity
Object two:
M = Mass
V = Velocity
I'll use the subscript i to denote initial velocity (i.e. velocity before collision) and subscript f for final velocity (velocity after collision). So vi is intial velocity of object one, Vf is final velocity of object two, etc. Mass doesn't change after collision, so doesn't need a subscript for before and after.
By conservation of momentum, the linear momentum of the system before = linear momentum after collision, that is momentum is conserved. [Not to say one of the particles in the system can';t come away with altered momentum, conservation of momentum applies to the system as a whole, or of a closed isolated system, which here is just two particles].
Algebraically:
mvi + MVi = mvf + MVf (Total momentum
before = total momentum after)
simplifying:
m(vi - vf) = -M(Vi - Vf) Equation
1.
Energy is also conserved, although for inelastic collision may end up as heat energy or doing work on the bodies and stored as potential energy, so total kinetic energy may be reduced (perhaps descibed a little inaccuratly as the bodies slowing a little afterwards). For these types of lossy inelastic collisions a coefficient of restitution is used (found experimentally for the materials in question). It's easy to add this co-efficient later, for now we assume for the sake of simplicity that kinetic energy is conserved (which generally it is not). Other derivations of the collision response formula take losses into account from the onset with this co-efficient, which actually simplifies and generalises things, there's lots of ways of coming up with the same answer.
Assuming an elastic collision, where kinetic energy is conserved:
mvi*vi/2 + MVi*Vi/2 = mvf*vf/2
+ MVf*Vf/2 (KE before = KE after)
simplifying:
m(vi*vi - vf*vf) = -M(Vi*Vi - Vf*Vf)
or
m(vi - vf)(vi+vf) = - M(Vi - Vf)(Vi+Vf) Equation 2.
[In non ASCII, neater would be using subscripts and the squared sign of course].
After dividing equation 2 by equation 1, and a little more algebra, the final
velocities are given by :
vf = vi*(m-M)/(m + M) + 2MVi/(m+M)
Vf = 2mvi/(m+M) + Vi(M-m)
And they are the forms of equations that a physics book would likely leave them. Halliday and Resnik "Fundamentals of Physics" is an excellent introductory undergrad physics text, showing this same derivation.
But with a little more algebra, the formulas could also be written:
vf = vi - 2M(vi-Vi)/(m+M) and
Vf = Vi+ 2m(vi-Vi)/(m+M)
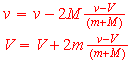
Example: Object A - Mass =1 Velocity =3 Object B - Mass =2 Velocity =-3 Object As final velocity = 3 - 2*2*(3+3)/3 = - 5 Object Bs final velocity = -3 + 2*1*(3+3)/3 = 1 |
To add to them, in vector form these would be:
vf = vi - 2M(vi-Vi).n/(m+M) n
Vf = Vi+ 2m(vi-Vi).n/(m+M) n
where n is the normal to the collision point, no time to go into this (for info about normals, see my page here - Martin).
(I should add that these equations are based on my own derivations and notes therefrom, not from a referenced source, so better would be to use a non-rushed source [e.g. Hecker], which with a little algebra mine should tie up. Partly shown below).
Impulse.
j = -(1+e)(v-V).n / (n.n(1/m + 1/M) where j is the impulse, e is the co-efficient
of restition (e=0 if inellastic, e=1 for elastic collision).
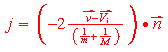
The formulas then become
vf = vi + jn/m and
Vf = Vi - jn/M
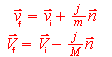
Example with figures as before: v = (3,0,0) V = (-3,0,0) and normal n = (-1,0,0)
Object As final velocity = (3,0,0) + 8 (-1,0,0) = (-5,0,0) Object Bs final velocity = (-3,0,0) - 4 (-1,0,0) = (1,0,0) |
All the above assumed an elastic collision and that n was normalised (unit length). Adding a coefficient of restitution (e) and using a non-unit length normal, the final equations are:
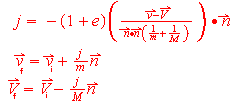
These do not account for rotation, though should tie up with the Hecker response equations. Rotation would take a lot more work. My own approach, at least before I started reading up on this stuff was different from sources that I've yet come across (and not yet as general), so no need to go into that...
Which look similar in form to that given by an impulse based approach, which I could also show but ASCII algebra is wearing me down. It's also a simple enough to convert these equations into vector form, so to work in 2 or more dimensions (excluding rotation), but this is probably better shown by an impulse method.
Hope the ASCII was readable, and no errors, my own ASCII is difficult to check :) (as you can see I have now added your graphics - Martin)
Regards
By: martinbaker ( Martin Baker )
RE: Greetings, nice site!
2002-12-22 08:43
Thank you,
This is very useful, I hope you don’t mind, I have put it at
https://www.euclideanspace.com/physics/dynamics/collision/steve.htm
and linked it from the other collision pages. I have made some attempt at formatting
it but not fully.
I’m sorry I don’t know your name (Sourceforge Discussion Forums don’t
include your name unless you login) I would be happy to include your name, or
if you want to remain anonymous that’s fine too.
When you say its one dimensional do you mean that it could be 2 or 3 dimensional, provided that the objects are constrained not to rotate (otherwise there would be no point in including the normal n). If I’m right in this assumption can I assume that where you have shown ‘.’ This is a dot product and all other multiplications are cross products?
Thanks,
Martin
By: nobody ( Nobody/Anonymous )
RE: Greetings, nice site!
2002-12-22 13:52
Hi Martin,
I didn't bother to register my name, partly because I didn't feel a need, and was quicker, and partly in case of spam :) I've given my name below though.
I don't mind you linking to what I wrote, although I it may be confusing in that hurried discussion type form. I'm easy, whatever you feel is best. I've created a .GIF
http://www.sriley.co.uk/deleteme/collision.gif of the formulas in a more friendly form (I don't have a simple method of converting math to HTML, how do you do it?). I wouldn't expect you to use the GIF (it's not maintainable like that anyway), but it should hopefully be much clearer for you to read than the ASCII. It'll likely disappear in the future, so a link to it wouldn't be a good idea. (I have taken this GIF, chopped it up and put it the equations above - Martin)
The vector forms of the equations work in 2 or 3 dimensions, but of course account only for *linear* energy/momentum, of which they account fully. For rotation (a lot) more needs to be done, as you know. So there would be no rotations, the resulting collision would behave like two point masses hitting each other. The formulas could be used for 2D/3D spheres though for example, if no rotation is required. I wrote some 2D applets along these lines some time back, e.g. : http://www.sriley.co.uk/Bounce2.html , http://www.sriley.co.uk/Cradle.html and even in 3D, e.g. : http://www.sriley.co.uk/OPENGL where I actually preferred not to account for rotation or friction in the simulation (well that's my excuse :). The next step is of course to go the whole way, and the final forms of the equations to account for everything are similar, but larger, and need more background to understand (setting up inertia tensors, etc, as you know and as described in the Hecker articles).
The normal in 2D or higher is still necessary to account for the applicable velocity, which for example in the case of spheres will be along a line joining their centres (which there also goes through the collision point). For instance a ball going at high speed brushing past another will hardly affect either velocity - the velocity normal is low. Describing the equation in words: Find relative velocity of A and B, and project this onto the nomal, this is how fast they are approaching each oher, and what is relevent to a collision. The rest of the equation is just the regular 1D stuff. A normal would also be required if bouncing off walls etc, unless the wall orientations are hard-coded into the program which is okay but would get messy for arbitrarily oriented lines/planes.
Hopefully now that the formulae are more readable, it can be seen there are no cross products. Impulse is a scalar (as is mass), so where they are multiplying it is a scalar times a vector, and the dot products now have a nice big dot :)
Hope this helps.
Regards
Stephen Riley
By: nobody ( Nobody/Anonymous )
RE: Greetings, nice site!
2002-12-22 14:17
Hi Martin,
Incidentally the collision response equations for 2D including angular affects
are also quite simple, illustrated by Hecker (sorry to keep referencing him)
at http://www.d6.com/users/checker/dynamics.htm
"Physics, Part 3: Collision Response".
Regards
By: nobody ( Nobody/Anonymous )
RE: Greetings, nice site!
2002-12-22 16:23
Hi Martin,
After reflecting on your comment on cross products, I realised I'd made a couple of mistakes in my comments. Interestingly they also tie up with your related comment on rotation as a constraint.
Impulse, being a change in momentum is a vector of course, not a scalar as I'd mentioned. But if impulse is only taken in the normal direction (the constraint of no rotation/friction) , j can be a scalar as above. So (and expanded upon below) the formulae work above with j as a scalar, my comment was just wrong. The other error, as a consequence of this oversight, was mentioning that Chris Heckers formulas account for friction, which they can't with j a scalar, since a frictional force would be tangent to the collision normal and would transfer momentum along that tangent. The fact that we don't have rotation after impact eliminates friction as a force as used above I would say anyway, so it ties up, but as mentioned, no rotation, and now definitetly no friction in that form.
I hadn't noticed j turning into a scaler in his derivation before, having not bothered much with friction in the past, and doing collisions my own way (the way I'd described first) sorry about the oversight, and well spotted!
Regards
By: martinbaker ( Martin Baker )
RE: Greetings, nice site!
2002-12-23 10:14
Yes, its tricky working with equations, there are a few things in HTML that
help like <sub> and <sup> tags and a few special characters, but
with these type of equations I usually end up having to use gifs.
I have therefore taken the your gif and extracted each equation into a separate
gif, then inserted these into the appropriate point in:
https://www.euclideanspace.com/physics/dynamics/collision/steve.htm
I also put a bar above the vectors and added f and i suffixes. I think I still need to tidy it up a bit more because I still have the old form of the equations in addition to the gifs.
I’m not sure it’s a good idea to tidy things up too much though, I quite like the idea of leaving in the working and to show some of the thought processes involved. Also I need as much help that I can get with the site, so I would like the site to look like a group effort, to encourage others to contribute.
Martin
By: nobody ( Nobody/Anonymous )
RE: Greetings, nice site!
2002-12-23 14:32
Hi Martin,
At this rate your site is going to be massive! But great to have around since for parts what you cover, there is little information, without pouring over texts like Goldstein, or discussion elsewhere . Having looked at some of the other comments, I can say I look forward to Todds' article on "Why angular momentum is the way it is" - what a great title!
cya for now (life's mundanities beckon)




