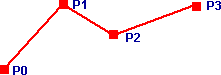
Geometrys are usually created from polygons. The edges of these polygons are straight lines connecting up the vertex coordinates. How do we make curved, organic looking surfaces, normals help to reduce the look of the sharp edges but do not change the angular shape of the outline.
One way to do this is to generate curved surfaces mathematically by using the vertices as control points. There are a number of methods to do this as described in the following sections:
Another use for this type of curve fitting is in animation, where we want to change some variable such as position over time.
Bezier Curves
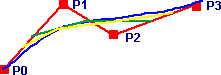
(cubic) Bezier curves can be generated recursively by joining up the midpoints of the lines joining the midpoints. The equation of this curve is given by:
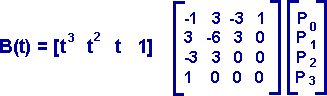
or
B(t) = (1-t)^3 p0 + 3t(1-t)^2 p1 + 3t^2(1-t) p2 + t^3 p3
B-Spline
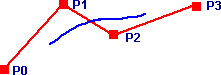
The generated curve does not necessarily pass through the control points, however if B-splines are calculated for adjacent sets of control points the curve segments will join up and produce a continuous surface. The equation for B-spline is:
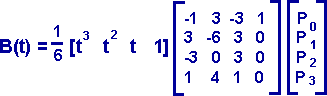
or
B(t) = 1/6 (-p0 + 3p1 -3p2+ p3)t^3 + 1/2 (p0 - 2p1 + p2) t^2 + 1/2 (-p0 + p2) t + 1/6 (p0 +4p1 + p2)
NURBS (Non-Uniform Rational B-Spline)
This allows a curvy surface to be rendered directly, without first generating a tessellated surface. This uses control methods called evaluators. NURBS is supported by OpenGL.


