Maths - Conversion Quaternion to Euler

Definition of terms:

• Euler Angles
• Quaternions

Java code to do conversion:

This depends on what conventions are used for the Euler Angles. The following assumes NASA Standard Airplane

/** assumes q1 is a normalised quaternion */

public void set(Quat4d q1) {
    double sqw = q1.w*q1.w;
    double sqx = q1.x*q1.x;
    double sqy = q1.y*q1.y;
    double sqz = q1.z*q1.z;
    heading = Math.atan2(2.0 * (q1.x*q1.y + q1.z*q1.w),(sqx - sqy - sqz + sqw));
    bank = Math.atan2(2.0 * (q1.y*q1.z + q1.x*q1.w),(-sqx - sqy + sqz + sqw));
    attitude = Math.asin(-2.0 * (q1.x*q1.z - q1.y*q1.w));
}

Note1: I have replaced Math.atan(a/b) with Math.atan2(a,b) as suggested by Mark Elson

Note2: minorlogic has said that the above expressions for heading and bank dont require q1 to be normalised, but the expression for attitude does. Andy has suggested including the normalisation in the attitude expression as follows (this saves a CPU heavy square root operation).

/** q1 does not need to be normalised*/
public void set(Quat4d q1) {
   double sqw = q1.w*q1.w;
   double sqx = q1.x*q1.x;
   double sqy = q1.y*q1.y;
   double sqz = q1.z*q1.z;
   heading = Math.atan2(2.0 * (q1.x*q1.y + q1.z*q1.w),(sqx - sqy - sqz + sqw));
   bank = Math.atan2(2.0 * (q1.y*q1.z + q1.x*q1.w),(-sqx - sqy + sqz + sqw));
   attitude = Math.asin(-2.0 * (q1.x*q1.z - q1.y*q1.w)/(sqx + sqy + sqz + sqw));
}

Derivation

Thank you Andy for the following. Comparing the matrix derived above to the matrix expressed in the quaternion component terms from the quaternionToMatrix page, we can derive the quaternion to Euler transformations on your quaternionToEuler page:

so that

Likewise,

  so 

and

so

These transformations are fully self-consistent and can be verified by substituting the Euler angle expressions for the quaternion components. For example, take the expression for q:

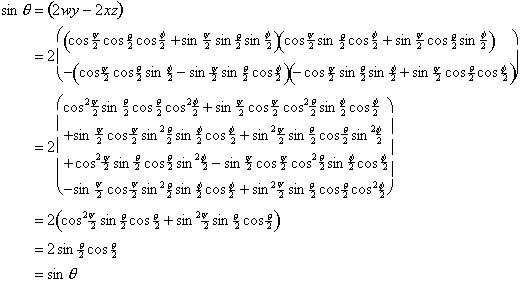
Similar, but messier, verifications can be done for the other two angles:

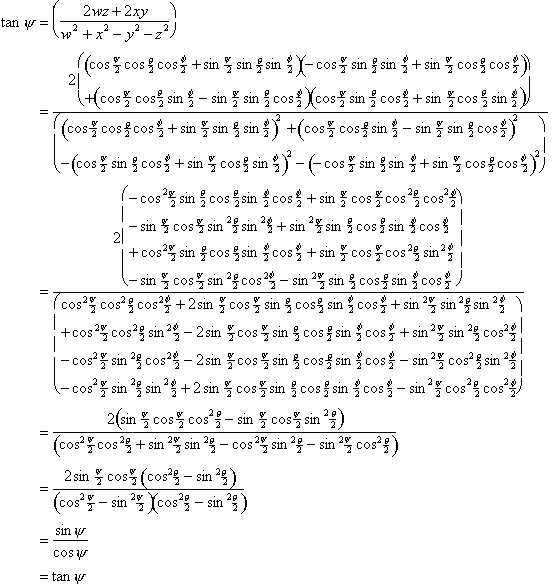
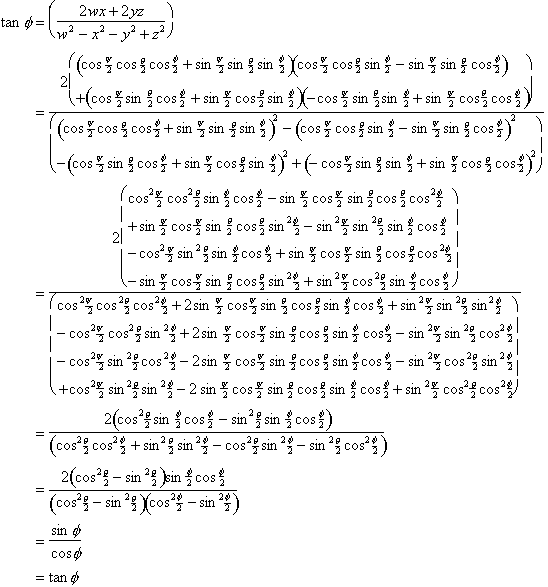
Issues

• It is better to use atan2 function than atan function as described here.
• For issues concerning asin and atan see here.
• Most trig functions (except openGL) use radians not degrees.

The trig functions are many to one, therefore the inverse trig functions have many possible results. We usually assume that:
acos returns the angle between 0 an pi
asin returns the angle between -pi/2 an pi/2
atan returns the angle between -pi/2 an pi/2

This is what the java Math functions return for instance. I think this makes sense in the context of finding euler angles because we would usually want to rotate the shortest angle to rotate.

Example

we take the 90 degree rotation from this:

to this:

As shown here the quaternion for this rotation is: (0.7071+ i 0.7071)

So using the above result:

sqw = q1.w*q1.w = 0.5
sqx = q1.x*q1.x = 0.5
sqy = q1.y*q1.y = 0
sqz = q1.z*q1.z =0
heading = atan2(2.0 * (q1.x*q1.y + q1.z*q1.w),(sqx - sqy - sqz + sqw)) = atan2(0,2) = 0
bank = atan2(2.0 * (q1.y*q1.z + q1.x*q1.w),(-sqx - sqy + sqz + sqw)) = atan2(0.5,0) = 90 degrees
attitude = asin(-2.0 * (q1.x*q1.z - q1.y*q1.w)/sqx + sqy + sqz + sqw) = asin(0/2) = 0

So this gives the correct result shown here, it is banking by 90 degrees, but we have to be very careful about the following issues:

• If we had not used the atan2 function then one of the intermediate steps would involve infinity (division by 0) therefore most maths libraries have an atan2 function to avoid this step.
• Most maths libraries use radians instead of degrees (apart from OpenGL).