The Div operator takes a vector field as an input and returns a scalar field representing how much the field is expanding or being created (i.e. how much it is diverging) at each point.
If:
v = vx i + vy j + vz k
Then div(v) is defined as:
| div(v) = | ∂vx | + | ∂vy | + | ∂vz |
| ∂x | ∂y | ∂z |
Where:
- vx= a scalar representing the component of v in the x direction.
- vy= a scalar representing the component of v in the y direction.
- vz= a scalar representing the component of v in the z direction.
Physical interpretation
If you measure gas flowing along a pipe, it is not diverging at all, and would have zero divergence. If you measure the flow of gas coming out of the pipe, then the flow would diverge, and you would have a non-zero value of div.
For an incompressible fluid such as water, which is flowing, but not being created or destroyed, then its divergence is zero at every point.
Imagine a cube at some point in space:
If we take total volume of fluid flowing out of the surface of the cube divided by the volume of the cube. The divergence at that point is the limit of this ratio, as the size of the cube tends to zero.
The volume of fluid flowing out of the surface is the volume flowing out of each of the six faces minus the volume flowing into each of the six faces.
In other words if there is the same amount flowing into one face as there is flowing out of the opposite face, then the total volume of fluid flowing out of the surface is zero.
Flow lines
If we have a moving fluid for example, and we plot out the lines that the particles are moving along:
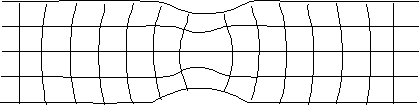
If the fluid is incompressible, a liquid say, then the fluid will have to flow faster at the constriction in the pipe. So that the volume of the cubes remains the same and div(v) remains zero.
If the fluid is compressible then, the cubes will get smaller and div(v) will be negative before the constriction and positive afterward.
Vector Operator
When we were looking at grad we defined the del symbol is used to represent the vector operator, as follows:
| ∂ | + j | ∂ | + k | ∂ | |
| ∂x | ∂y | ∂z |
This operator can also be used for divergence, but this time using dot multiplication:
![]() • v
= div(v)
• v
= div(v)
Identities
div of vector field multiplied by scalar field:
div(s v) = s div(v) + v grad(s)
div of cross product of two vector fields:
div (v1 × v2) = v2• curl(v1) - v1• curl(v2)

