| type | f(x) | d f(x) / dx |
|---|---|---|
| constant | a | 0 |
| power | xn | n*xn-1 |
| exponential | ex | ex |
| trig functions | sin(x) | cos(x) |
| cos(x) | -sin(x) | |
| tan(x) | sec2(x) | |
Derivation
Possibly the easiest way to derive these results is to convert the function into an infinite series, then differentiate the terms separately, then convert back to a function.
Alternatively we can often derive the results geometrically.
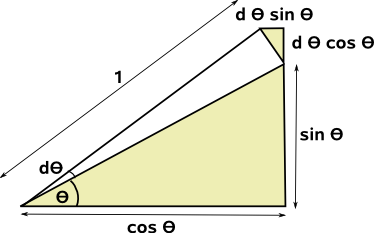
as we can see from the above construction, by congruent triangles:
d (sin θ) = dθ cos θ
and
d (cos θ) = - dθ sin θ
which gives:
d (sin θ)/dθ = cos θ
and
d (cos θ)/dθ = -sin θ


