Maths - Quaternion Calculus

Quaternion Differentiation with respect to Scalar

To differentiate a quaternion with respect to a scalar, say 'x', we individually differentiate each element with respect to 'x'. So if:

f(x) = a + b i + c j + e k

then:

d f(x) / dx = d(a /dx) + d(b/dx) i + d(c/dx) j + d(e/dx) k

So to give a more specific example if:

f(x) = xⁿ + sin(x) i + tan(x) j + e^x k

then:

d f(x) / dx = n*x^n-1 + cos(x) i + sec²(x) j + e^x k

So this is quite simple, provided that we can differentiate the elements of a quaternion, we can differentiate the whole quaternion.

Quaternion Differentiation with respect to another Quaternion

Since division of one quaternion by another will give a result for non-zero values (unlike vectors) we can define differentiation with respect to another quaternion.

What are the rules of such differentiation? What applications does it have?

Could we use it in this situation? Imagine that two quaternions represent the angular position of two gears, can we differentiate one with respect to another to get the ratio of the gears?

Applications

Here we go back to the simple case of differentiation with respect to scalars, when we start to look at applications it becomes less simple.

For instance, with linear movement we just use v = dx/dt and we treat velocity v as being the same thing as dx/dt but with rotation the equation is more complicated: 
d q(t) /dt = 1/2 * W(t) q(t)

This is also discussed on the angularvelocity page 
 
What I want to do is understand the deeper reasons for this extra complexity. I think this involves these factors:

• These are time varying quantities, of course v = dx/dt works for time varying quantities but at least if we have constant velocity (and so constant linear momentum) then dx/dt will be constant. But if q(t) represents the orientation of an object rotating at a constant angular velocity (and constant angular momentum) then d q(t)/dt will still vary with time but W(t) will not vary with time and therefore is a better representation of angular velocity.
• I think differentiation is related to the addition operation but rotations are combined using quaternion multiplication, not addition. When I say "differentiation is related to the addition operation" I mean: when we add a small increment to time we get a small increment to distance, differentiation is the limit when these additions. So is there a mathematical theory that relates small incremental multiplications to conventional differentiation?

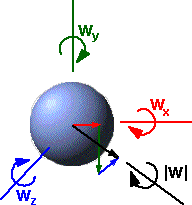
Imagine a solid object which has simultanous rotation about the x,y and z axes, the angular velocity about these axes is w_x,w_y and w_z. This rotation could also be represented by a single rotation about the axis w_x+w_y+w_z, this axis can be normalised to give u =( i w_x²+j w_y²+k w_z²)/ |w(t)|. The magnitude of the rotation about this axis is |w(t)| = sqrt(w_x²+w_y²+w_z²).

Now, in the time interval dt the angle turned will be:

|w(t)|dt

let angle turned in dt, expressed as a quaternion be:

q = (cos(|w(t)|*dt/2),u sin(|w(t)|*dt/2))

where:

• |w(t)| = sqrt(w_x²+w_y²+w_z²)
• u =( i w_x+j w_y+k w_z )/ |w(t)|

The quaternion of this angle is:

q = cos(|w(t)|*dt/2) + i sin(|w(t)|*dt/2)*w_x/|w(t)| + j sin(|w(t)|*dt/2)*w_y/|w(t)| + k sin(|w(t)|*dt/2)*w_z/|w(t)|

so since i,j and k are constants,

dq/dt = d cos(|w(t)|*dt/2)/dt + i d sin(|w(t)|*dt/2)*w_x/|w(t)| / dt + j d sin(|w(t)|*dt/2)*w_y/|w(t)| / dt + k d sin(|w(t)|*dt/2)*w_z/|w(t)| / dt

	useful differentials:
d cos(|w(t)|*dt/2)	= -sin(|w(t)|*dt/2) (d (|w(t)|*dt/2) /dt) = -0.5*sin(|w(t)|*dt/2) (d wx + d wy + d wz)
d sin(|w(t)|*t/2)wx/|w(t)|	= cos(|w(t)|*dt/2)*(d (|w(t)|*dt/2) /dt)*wx/|w(t)| = 0.5*cos(|w(t)|*dt/2) wx/|w(t)| d |w(t)|
d sin(|w(t)|*t/2)wy/|w(t)|	= cos(|w(t)|*dt/2)*(d (|w(t)|*dt/2) /dt)*wy/|w(t)| = 0.5*cos(|w(t)|*dt/2) wy/|w(t)| d |w(t)|
d sin(|w(t)|*t/2)wz/|w(t)|	= cos(|w(t)|*dt/2)*(d (|w(t)|*dt/2) /dt)*wz/|w(t)| = 0.5*cos(|w(t)|*dt/2) wz/|w(t)| d |w(t)|

dq = -0.5*sin(|w(t)|*dt/2)(d w_x + d w_y + d w_z)
+ i (0.5*cos(|w(t)|*dt/2) wx/|w(t)| d |w(t)|)
+ j (0.5*cos(|w(t)|*dt/2) wy/|w(t)| d |w(t)| )
+ k (0.5*cos(|w(t)|*dt/2) wz/|w(t)| d |w(t)|)

= - (wx + wy +wz)*sin(|w(t)|*dt/2)/|w(t)| + i (wx*cos(|w(t)|*dt/2) + j ( wy*cos(|w(t)|*dt/2) + k ( wz*cos(|w(t)|*dt/2))

= - wx*sin(|w(t)|*dt/2)*w_x/|w(t)| -wy* sin(|w(t)|*dt/2)*w_y/|w(t)| - wz*sin(|w(t)|*dt/2)*w_z/|w(t)|
+ i (wx*cos(|w(t)|*dt/2) + wy*sin(|w(t)|*dt/2)*w_z/|w(t)|- wz*sin(|w(t)|*dt/2)*w_y/|w(t)| )
+ j ( - wx*sin(|w(t)|*dt/2)*w_z/|w(t)|+ wy*cos(|w(t)|*dt/2) + wz*sin(|w(t)|*dt/2)*w_x/|w(t)|)
+ k ( wx*sin(|w(t)|*dt/2)*w_y/|w(t)| - wy*sin(|w(t)|*dt/2)*w_x/|w(t)| + wz*cos(|w(t)|*dt/2))

= - wx*sin(|w(t)|*dt/2)*w_x/|w(t)| -wy* sin(|w(t)|*dt/2)*w_y/|w(t)| - wz*sin(|w(t)|*dt/2)*w_z/|w(t)|
+ i (wx*cos(|w(t)|*dt/2) + wy*sin(|w(t)|*dt/2)*w_z/|w(t)|- wz*sin(|w(t)|*dt/2)*w_y/|w(t)| )
+ j ( - wx*sin(|w(t)|*dt/2)*w_z/|w(t)|+ wy*cos(|w(t)|*dt/2) + wz*sin(|w(t)|*dt/2)*w_x/|w(t)|)
+ k ( wx*sin(|w(t)|*dt/2)*w_y/|w(t)| - wy*sin(|w(t)|*dt/2)*w_x/|w(t)| + wz*cos(|w(t)|*dt/2))

= 0.5 (0 + i wx + j wy + k wz ) * (cos(|w(t)|*dt/2) + i sin(|w(t)|*dt/2)*w_x/|w(t)| + j sin(|w(t)|*dt/2)*w_y/|w(t)| + k sin(|w(t)|*dt/2)*w_z/|w(t)| )

0.5*w(t)*q(t)

where:

• w(t) = 0 + i wx + j wy + k wz
• q(t) = cos(|w(t)|*dt/2) + i sin(|w(t)|*dt/2)*w_x/|w(t)| + j sin(|w(t)|*dt/2)*w_y/|w(t)| + k sin(|w(t)|*dt/2)*w_z/|w(t)|

---

So:

dq/dt = 0.5*w(t)*q(t)

where:

w(t) = 0 + i wx + j wy+ k wz

 

w(t) is a quaternion representing angular velocity = θ(t)*u(t) = (dq/dt) * q^-1

Any angular velocity can be represented by an axis and a rotation dθ/dt about that vector (similar to axis and angle but instead axis and angle/sec). This is an instantaneous angular velocity, if there is a net torque then both dθ/dt and the axis direction may be changing, in other words they may both be functions of time.

---

Quaternion integration

As with differentiation we can integrate a whole quaternion by individually integrating each element. So if:

f(x) = a + b i + c j + e k

then:

∫ f(x) dx = (∫a dx) + (∫b dx) i + (∫c dx) j + (∫e dx) k

EuclideanSpace

home

Prerequisites

If you are not familiar with quaternion algebra you may like to look at the following pages first:

• quaternion algebra

Quaternion Physical Interpretation

Calculus