A Binary Space Partitioning (BSP) tree is a data structure that represents a recursive, hierarchical subdivision of n-dimensional space into convex subspaces. BSP tree partitions space by any hyperplane that intersects the interior of that subspace. The result is two new subspaces that can be further partitioned recursively.
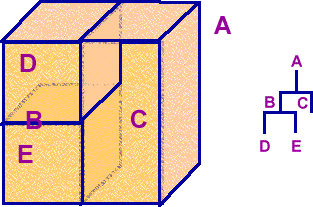
For example, the 3D space A is divided into B and C, B is then further subdivided into D and E.
BSP trees can be used for sorting and classification structures. They can be used for:
- hidden surface removal
- ray tracing hierarchies
- solid modeling
- robot motion planning.
Solid modeling methods with BSP trees
A three dimensional volume could be modeled by dividing the world into small cubes (see voxel), the position of each cube could be represented by 3 Cartesian coordinates (x,y and z) and if each cube were small enough then it could be considered to contain only one type of matter coded in some way. However this would require an enormous array of data to hold a reasonable representation of a scene. This might be an inefficient way to model the world because a large mass of homogenous matter would require just as much data as the very intricate parts of its outer structure. Therefore it might be more efficient to hold this information in a BSP tree or an octtree, then we can have lots of detail in the parts that need it, without wasting data where it is not needed.
BSP trees are not usually the mechanism that holds the shape. Other methods such as triangles or polygons model the shape, BSP trees are then applied to this to do hidden surface removal or ray tracing, etc. If a partition plane crosses a triangle/polygon then the polygon is split so that no polygon is in more that one partition.
BSP trees can be used for solid modeling in the following ways:
- Incremental construction - Incremental construction of a BSP Tree is the process of inserting convex polytopes into the tree one by one.
- Tree merging
Choosing the partition plane
The choice of partition plane depends on how the tree will be used, and on your efficiency criteria. Options are:
- Choose the partition plane from the input set of polygons (called an autopartition).
- Axis aligned orthogonal partitions.
It can help efficiency to have a balanced tree, where each leaf contains roughly the same number of polygons. However, there can be a cost in achieving this. If a polygon happens to span the partition plane, it will be split into two or more pieces. A poor choice of the partition plane can result in many such splits, and a marked increase in the number of polygons. There may be a trade off between a well balanced tree and a large number of splits.
Partitioning polygons
Partitioning a set of polygons with a plane is done by classifying each member
of the set with respect to the plane. If a polygon lies entirely to one side
or the
other of the plane, then it is not modified, and is added to the partition set
for the side that it is on. If a polygon spans the plane, it is split into two
or more
pieces and the resulting parts are added to the sets associated with either
side as appropriate.
When to stop
The decision to terminate tree construction is, again, a matter of the specific application. Some methods terminate when the number of polygons in a leaf node is below a maximum value. Other methods continue until every polygon is placed in an internal node. Another criteria is a maximum tree depth.
Painter's algorithm
The idea behind the painter's algorithm is to draw polygons far away from the eye first, followed by drawing those that are close to the eye. Hidden surfaces will be written over in the image as the surfaces that obscure them are drawn. One condition for a successful painter's algorithm is that there be a single plane which separates any two objects. This means that it might be necessary to split polygons in certain configurations. For example, this case can not be drawn correctly with a painter's algorithm:
