This page is supplied by Richard
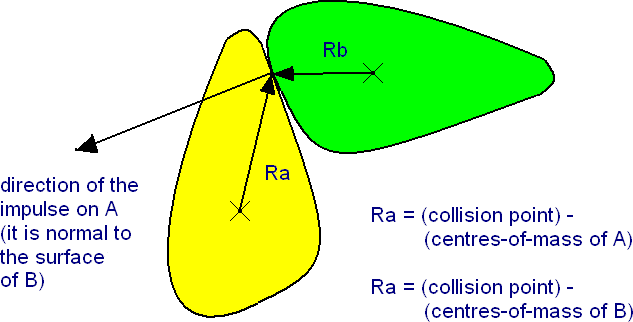
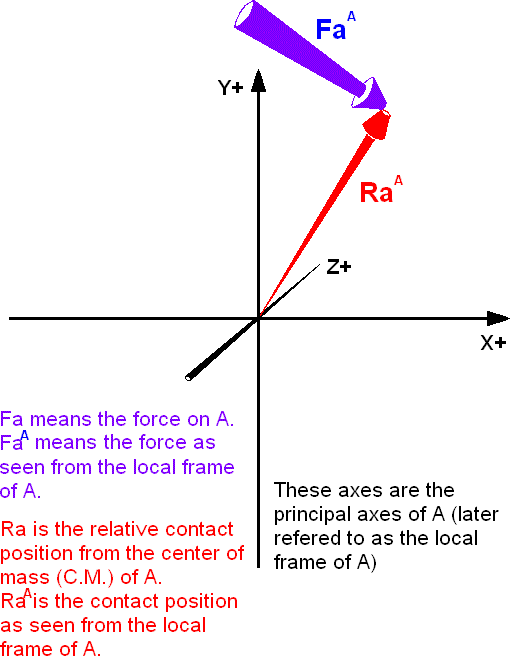
Rigid body A (on left) collides with rigid body B (on right). An equal but opposite impulse is felt on A and B. The impulse on A is in the same direction as the normal reaction Na away from the surface of B, visa versa the impulse on B is in the same direction as the normal reaction away from the surface of A, or simply in the direction of -Na. Na will later be referred to as just N which is directed towards A.
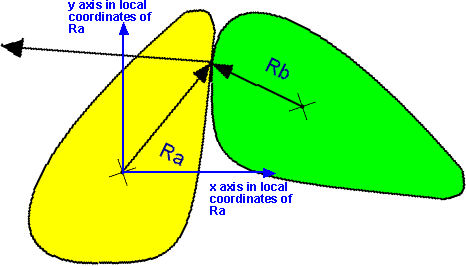
The local frame of rigid body A
Direction of Rotation
Consider the Z component of the force, Fz, and this component alone.
And look in the +Z direction in the frame of A.
Now Fz can either be + or -, that is, into the screen or out of the screen respectively. A dot (.) means that it is out of the screen, and a cross (x) means that it is into the screen.
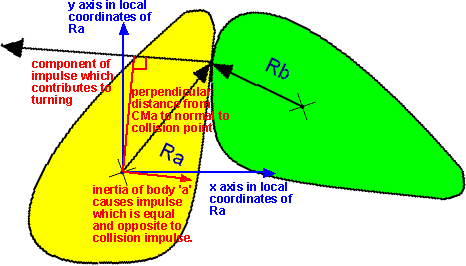
The components of R which form perpendicular moments with the force, Fz, are Rx and Ry.
The rotations about the X and Y axes can be shown to depend on the moments -(FzRy) and +(FzRx) respectively.
If we say that a positive rotation about X is a clockwise rotation, when we
look along the X axis using our coordinate system, then confirm from
the diagram that -(FzRy) is a measure of the clockwise rotation.
Use Fz= +1, Ry= +1 Rotation about X is anti-clockwise
Use Fz= -1, Ry= +1 Rotation about X is clockwise
Use Fz= +1, Ry= -1 Rotation about X is clockwise
Use Fz= -1, Ry= -1 Rotation about X is anti-clockwise
Likewise +(FzRx) is a measure of the clockwise rotation about Y
Use Fz= +1, Rx= +1 Rotation about Y is clockwise
Use Fz= -1, Rx= +1 Rotation about Y is anti-clockwise
Use Fz= +1, Rx= -1 Rotation about Y is anti-clockwise
Use Fz= -1, Rx= -1 Rotation about Y is clockwise
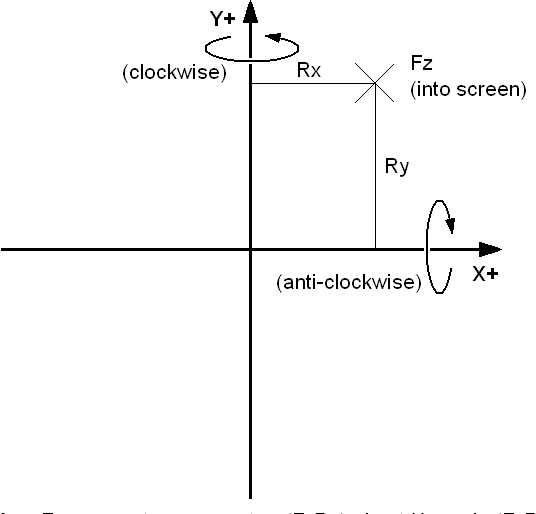
Therefore Fz causes two moments, -(FzRy) about X and +(FzRx) about Y.
Likewise, Fy causes -(FxRz) about Y and +(FxRy) about Z. and Fx causes -(FyRx) about Z and +(FyRz) about X.
Therefore,
Moment about principle axis X = FyRz - FzRy
Moment about principle axis Y = FzRx - FxRz
Moment about principle axis Z = FxRy - FyRx
Description of method
This is is an outline of the theory.
Two rigid bodies collide in 3d. Their mass, principle moments of inertia, velocity, angular velocity, position and orientation are known. Adding to what is known is the normal of their surfaces at the collision point between them.
The impulse on the bodies will act in the normal to the contact point C. Now put yourself in the local frame of body A. U will see the normal rotated against the orientation of A. Since your perspective in the local frame, then T = [I]a where [I] is the tensor in the local frame and a is the angular acceleraton vector, a is in the loacl frame and the torque T is in the local frame. (Maybe I should have written T with a superscript to show it is in the local frame).
|
Futher information, questions etc. by Martin
I guess that in the local frame of reference of 'a' the positions and velocities will all be modified. If 'a' is rotating then the other objects will appear to be spiralling around it, all these distances an velocities will be a function of time and it will not be an inertial reference frame so we will need to be careful about applying F=ma and T = [I]a. I don't know if this is an issue, I have just put this temporary note here to remind me to think about it. - MJB Richard has pointed out that in the instant that the collision occurs the momentum (and hence the velocities) are considered to change instantanously but the positions don't change in that instant. So we don't need to consider how the positions are a function of time. |
This in itselfs works out to Tx = Ix.ax , Ty =Iy.ay , Tz = Iz.az with angular accelaration given as ax = Tx/Ix , ay =Ty/Iy , az = Tz/Iz.
|
Only if the object is symetrical about the x,y and z cooridinates? otherwise do we need to use all 9 elements of the inertia tensor - Ixx, Ixy, Ixz, Iyx, Iyy, Iyz, Izx, Izy, Izz. - MJB |
To calculate the torque, we use T = F x R, but we first calculate the global torque, so in this case torque T is global, F and R are also global. We rotate the global T against the orientation of A to get the local T. Then we find the local vector [ax, ay, az]. So far we have just generalized our input data.
|
It seems to me that there are two forces (impulses) on body 'a'. The component of impulse in direction of normal which contributes to turning and an equal and opposite value acting on the centre of mass.
So when we use F x R how to calculate F and R (I think I need to read and understand the bit below first). - MJB |
The next step is to calculate an apparent mass _M_ and an apparent acceleration _A_ .
This theory is base on the interaction of a translational frame and a rotatonal frame. Picture a model of the collision with a small linear spring between the colliding surfaces at the contact point. Since the spring is linear, it applies a force on the bodies, the bodies accelerate away, thus some apparent mass that is felt by the spring, depending on the objects linear acceleration at the conatct point.
In summary, this apparent mass is calculated from the local frame to be consistent. But we are only concerned with the line of action of the normal and the frame does not matter because in the end the result in dotproduct with the normal and we have a scalar which turn out to be squared and all positive. This is a long calculation but I did a 2d example.
I am quoting that here, consider that acceleration of the "contact point" in 2d:
The amount of linear acceleration caused by the tranlational frame= F/m
The amount of linear acceleration caused by the rotaional frame= a.R {the angular
acceleration times the vector from thecenter-of-mass to the contact point. In
3d, it is (R x a).N } = (T/I)R {Torque in the local frame divided by proncipal
moment of inertia}
= ((FR)/I)R {F and R are in the local frame}
= (F/m) *sq(R/r) {R is in the local frame. In 3d, it is ...sq((NyRz -NzRy)/rx...
with N and R being Nlocal and Rlocal}
In the last step, I was substituted where I=mrr and r is the radius of gyration
Therefore, the aggregate acceleration (from both translational and rotational
frame) _A_ is the sum of (F/m) and (F/m)*sq(R/r) or the accelerations in the
two frames. So,
_A_ = (1+ sq(R/r) * F/m
and _M_ = m /(1 +sq(R/r))
This result is positive and requires R to be in the local frame
In 3d,
_M_ = m / (1 + * squaremodulus(H))
where H = [(NyRz - NzRy)/rx , (NzRx - NxRz)/ry (NxRy - NyRx)/rz]
N and R in H must be the local values, however the term (NyRz - NzRy) is the
crossproduct-xterm of N and R. If we have Nglobal and Rglobal then Nglobal x
Rglobal gives NRglobal, and if we rotate the NRglobal against the orientation
of the body then we have NRlocal. and this will satisfy the terms in H.
So we used
(1) apparent acceleration _A_ and its mass _M_ are related by F = _M_ _A_ .
(2) the acceleration is the sum of the acceleration in the
translational frame and the rotational frame since the force acts in both frame
at the same time.
Now that we have _M_, we model the collision on the tiny spring and we only
see two apparent masses and two aproaching velocities. We can using any of
the equations of 1d rigid body collision because we have scalars that only depend
on direction positive or negative
If we choose
impulse = 2 * (Vbi - Vai) * (Ma Mb) / (Ma + Mb)
the Ma and Mb are the aparent masses of _Ma_ and _Mb_ respectively
(Vbi-Vai) is the aproaching velocity
This leads us (after some simplification) to
Impulse = 2 * (_Vbi_ - _Vai_) / ((1 + sqmod(Hb))/Mb + (1 + sqmod(Ha))/Ma)
and H is corrected for the local frame of rigid bodies, A and B.
From here, we want to know how much acceleration was caused by the individual
frames. So if we have an impulse given above, we know that our acceleration
of our translational frame was F/m and the similar proceedure with the rotaion.
It is like reverse engineering. I wote it up on paper and it seems long and
overkill, and I think it can be simplified. The important thing it to calculate
_M_ and this was done with the correct crossproduct convention and I hope that
you understand the frames now.
About the convention
X = Y x Z
Y = Z x X (this must holds if above holds using the same crossproduct
operation) Z = X x Y
T = F x R Torque is Force crossproduct ContactPointVector
A = R x a Linear acceleration is ContactPointVector crossproduct
AngularAcceleration
For T, F, R, A, a all being unit vectors in the direction of the specified axis, let us sat that:
X = T , Y = F , Z = R
and we use
X = Y x Z
but we know that also
Y = Z x X
so if Y = F = A (same direction) , Z = R , and X = T = a (same direction)
then A = R x a
A mechanism for collisions - masses, velocity and a spring
What happens when rigid bodies collide?
Let us look at two billiard balls approaching in a straight line, a and b, when they collide there is a reaction at the surface of the balls and this reaction is perpendicular to the surface at the contact point. a feels a reaction from b, and b feels the reaction from a. This reaction lasts as long as the balls are in contact with each other, and it causes the velocities of the balls to change continuously but in a very short time until the balls start to separate from each other.
The reaction comes from the contact point on the surface of the balls, and it causes an impulse from the very short duration of the collision. The impulse is noticeably related to how fast the balls were approaching and to how much mass they had. For greater masses and approaching velocities, there would be a greater reaction and/or duration of the reaction needed to cause the balls to separate, thus a greater impulse.
We know that the formula for impulse in this linear case to be impulse = 2 * (Vbi - Vai) * (Ma Mb) / (Ma + Mb) for a perfect elastic collision. Note the term for the approaching velocity and the terms for the masses.
Let’s take a look at the case when a and b are not billiard balls, but they are irregular rigid body objects. Nothing is different if they collide in such a way that the reaction passes through their center of masses. Their separation will be in a straight line and there will not be any rotation on the bodies.
Before we consider what happens when the reaction is not directed towards the center of mass, let us devise a mechanism that demonstrates collisions in general. We will not concern our selves with rotations and frames of reference; instead we will look only at the reaction at the surface of the bodies. Lets us pretend that a spring existed between the surfaces at the collision point. This spring gives the reaction force. The reaction and its duration still depend on how fast the surfaces of a and b are approaching and how difficult it would be to separate the surfaces. The spring acts equally on both a and b so it does not introduce any new momentum into the system and the total momentum is always preserved. In other words the spring model conserves momentum. The spring sees two surfaces that approach at a particular speed, and then it reacts by slowing their velocities until the approaching velocity is 0. The spring now has potential energy for a very short time. Next it gives back the bodies the same amount energy, and conserves energy for a perfect elastic collision. It does this by making the separation velocity the same as the approaching velocity. Note that if it did not give back all the energy then momentum would be still conserved. A simple example is two balls of the same mass which are colliding in a straight line with equal magnitudes of velocities. Momentum is preserved if they (1) stick together or (2) separate at equal magnitudes of velocity. Energy is loss in (1) but in (2) energy would be preserved if the separation magnitude is the same as the approaching magnitude. If you have problems accepting the spring model then consider if there can be any other factor that can affect the amount of impulse caused by the spring other than how much it is compressed due to the continuous velocities of the surfaces of a and b and how quickly they can decelerate to reach zero approaching velocity in the first half of the collision. The spring models the impulse behavior by being dependent on the masses and approaching velocity.
Now that we have established a workable mechanism, let state that all we need to find the impulse in a collision are the masses and approaching velocity. In a general case the mass that the spring sees is simply a measure of how fast it will be able to accelerate the surface away. This can be calculated by applying a force in the direction of the spring on the rigid body and measuring how fast it moves away or the surfaces acceleration. Then we dived the force we applied by the acceleration to find a mass that is felt by the spring. To calculate the approaching velocity we would have to resolve the approaching velocity of the surfaces in the direction of the spring.
A generalized method for calculating that the spring sees
How fast will the contact point on surface of a accelerate in the direction of the force?
In general when a force acts on a rigid body, it produces a torque and a linear acceleration.
T = [I]a
Where [I] is the inertia tensor for the rigid body in the global frame, T is torque and a is angular acceleration in the global frame
Tx = Ixx*ax + Ixy*ay + Ixz*az
Ty = Iyx*ax + Iyy*ay + Iyz*az
Tz = Izx*ax + Izy*ay + Izz*az
The torque is also the cross product of the force F and the vector R where R is a vector from the center-of-mass of a to the contact point. F and R are in the global frame.
T = F x R
This equation expands to:
Tx = FyRz - FzRy
Ty = FzRx - FxRz
Tz = FxRy - FyRx
Let us equate the torque terms.
FyRz - FzRy = Ixx*ax + Ixy*ay + Ixz*az
FzRx - FxRz = Iyx*ax + Iyy*ay + Iyz*az
FxRy - FyRx = Izx*ax + Izy*ay + Izz*az
We are interested in the angular acceleration vector, but it is difficult to extract in this form.
Is it possible to rewrite the above equation in the local frame and it is still valid?
T = [I]a
T = O[Io]OTa
Where O is the orientation matrix, OT is the transpose of O and OT is same as the O-1 for orientation matrices.
OT T = [Io]OTa
Tlocal = [Io]alocal
It becomes simpler to calculate Tlocal and we use it in this equation to get alocal. First we calculate Tglobal and since T is a transformable vector we use (OT Tglobal) to calculate Tlocal. We then get alocal. We then calculate aglobal.
Now that we have the angular acceleration; we want to find out how fast the surface will accelerate in the direction of the spring.
Let this acceleration of the contact point in the direction of the spring be a scalar _A_. Note that since we resolve using the direction of the force on the body then we will get a positive value.
_A_ = (F/m).N + (a x R).N
where N, F, R, and a are in the global frame.
_A_ = |F|/m + (a x R).N
A generalized method for calculating the approaching velocity that the spring sees
Program
// RigidSim.cpp : Defines the entry point for the console application.
//
#include "stdafx.h" #include "Fl64Vector3d.h"
#include "Fl64Matrix3d.h"
#include <time.h>
#include <math.h>
#include <stdlib.h>
void CalculateAngularMomentum(const Fl64Vector3d & Wo, const Fl64Vector3d & Io, const Fl64Matrix3d & Oo, Fl64Vector3d & Lo)
{
// Angular momentum = Iw
Fl64Vector3d Woo; //This is Wo but as seen from the local frame of body o
Woo.MakeRotationOf_OtherVector_TransposeAnyMatrix(Wo, Oo);
Fl64Vector3d Loo; //Angular momentum as seen from the local frame of body o
Loo[0] = Io[0] * Woo[0];
Loo[1] = Io[1] * Woo[1];
Loo[2] = Io[2] * Woo[2];
Lo.MakeRotationOf_OtherVector_AnyMatrix(Loo, Oo);
}
void CalculateRotationalEnergy(const Fl64Vector3d & Wo, const Fl64Vector3d & Io, const Fl64Matrix3d & Oo, double & Ero)
{
Fl64Vector3d Woo; //This is Wo but as seen from the local frame of body o
Woo.MakeRotationOf_OtherVector_TransposeAnyMatrix(Wo, Oo);
// Rotational energy = 0.5 * Iww
Fl64Vector3d axiso;
axiso = Woo.GetNormal();
double Iaxiso;
Iaxiso = (Io[0]*axiso[0]*axiso[0]) + (Io[1]*axiso[1]*axiso[1]) + (Io[2]*axiso[2]*axiso[2]);
//Method 1
Ero = 0.5 * Iaxiso * (Woo.GetSquareMagnitude());
//Method 2
Ero = 0.5 * ( (Io[0] * Woo[0] * Woo[0]) +
(Io[1] * Woo[1] * Woo[1]) +
(Io[2] * Woo[2] * Woo[2]) );
} void CalculateLinearMomentum(const Fl64Vector3d & Vo, const double & Mo, Fl64Vector3d & Go)
{
// Linear momentum = Mv
Go = Mo * Vo;
}
void CalculateTranslationalEnergy(const Fl64Vector3d & Vo, const double & Mo, double & Eto)
{
// Translational energy = 0.5 * Mvv
Eto = 0.5 * Mo * (Vo.GetSquareMagnitude());
}
int main(int argc, char* argv[])
{
START:
{
/*
Create the Test data to be used in the simulation
The data contains 'velocity's and 'inertia's and the orientaions in the form of a matrix
The matrix will be explained to have so much rotation about the global axes so that this
orientation is understood just like position
*/
//'Velocity's
Fl64Vector3d Vai;
Fl64Vector3d Vbi;
Fl64Vector3d Wai;
Fl64Vector3d Wbi;
// Temps
Fl64Vector3d dVa;
Fl64Vector3d dVb;
Fl64Vector3d dWa;
Fl64Vector3d dWb;
// Results
Fl64Vector3d Vaf;
Fl64Vector3d Vbf;
Fl64Vector3d Waf;
Fl64Vector3d Wbf;
//'Inertia's
double Ma;
double Mb;
Fl64Vector3d Ia;
Fl64Vector3d Ib;
// Temps
Fl64Vector3d ra;
Fl64Vector3d rb;
// Orientations
Fl64Vector3d Qa; //This is a vector of the simultaneous rotation angles in radians
Fl64Vector3d Qb;
// Temps
Fl64Matrix3d Oa;
Fl64Matrix3d Ob;
// Normal from B to A
Fl64Vector3d N;
// Impact postion
Fl64Vector3d Ra;
Fl64Vector3d Rb;
/*
Initializing the test data
*/
time_t RandomSeed;
time(&RandomSeed);
srand(RandomSeed);
//#define RandomizeDby2(D) { D = pow((((rand() % 2000)/1000.0) - 1.0) * 2.0, 2.0) - 2.0;}
#define RandomizeDby2(D) { D = (rand() % 2000)/100.0;}
#define RandomizeVby2(V) { RandomizeDby2(V[0]);\
RandomizeDby2(V[1]);\
RandomizeDby2(V[2]);}
//'Velocity's
RandomizeVby2(Vai)
RandomizeVby2(Vbi)
RandomizeVby2(Wai)
RandomizeVby2(Wbi)
//'Inertia's
RandomizeDby2(Ma)
RandomizeDby2(Mb)
if(Ma < 0.0) Ma *= -1.0;
if(Mb < 0.0) Mb *= -1.0;
RandomizeVby2(Ia)
RandomizeVby2(Ib)
if(Ia[0] < 0.0) Ia[0] *= -1.0;
if(Ia[1] < 0.0) Ia[1] *= -1.0;
if(Ia[2] < 0.0) Ia[2] *= -1.0;
if(Ib[0] < 0.0) Ib[0] *= -1.0;
if(Ib[1] < 0.0) Ib[1] *= -1.0;
if(Ib[2] < 0.0) Ib[2] *= -1.0;
// Orientations
RandomizeVby2(Qa)
RandomizeVby2(Qb)
// Normal from B to A
RandomizeVby2(N);
N = N.GetNormal();
// Impact postion
RandomizeVby2(Ra)
RandomizeVby2(Rb)
/*
Evaluate Temps
*/
Oa.MakeRotateSimultaneousXYZ(Qa[0], Qa[1], Qa[2]);
Ob.MakeRotateSimultaneousXYZ(Qb[0], Qb[1], Qb[2]);
ra[0] = sqrt(Ia[0]/Ma);
ra[1] = sqrt(Ia[1]/Ma);
ra[2] = sqrt(Ia[2]/Ma);
rb[0] = sqrt(Ib[0]/Mb);
rb[1] = sqrt(Ib[1]/Mb);
rb[2] = sqrt(Ib[2]/Mb);
/*
Calculate the initial angular and linear momentum
*/
//'Momentum's
Fl64Vector3d Gai; //Initial linear momentum
Fl64Vector3d Gbi; //Initial linear momentum
Fl64Vector3d Lai; //Initial angular momentum
Fl64Vector3d Lbi; //Initial angular momentum
CalculateAngularMomentum(Wai, Ia, Oa, Lai);
CalculateAngularMomentum(Wbi, Ib, Ob, Lbi);
CalculateLinearMomentum(Vai, Ma, Gai);
CalculateLinearMomentum(Vbi, Mb, Gbi);
/*
Calculate the initial rotational and translational energy
*/
// Energies
double Erai; //Initial rotational energy
double Erbi; //Initial rotational energy
double Etai; //Initial translational energy
double Etbi; //Initial translational energy
CalculateRotationalEnergy(Wai, Ia, Oa, Erai);
CalculateRotationalEnergy(Wbi, Ib, Ob, Erbi);
CalculateTranslationalEnergy(Vai, Ma, Etai);
CalculateTranslationalEnergy(Vbi, Mb, Etbi);
/*
Simulate Kinematics
*/
double _Vba_;
//Calculate the approaching velocity of B as seen from the direction from B to A
//(Vb + (Rb x Wb) - Va - (Ra x Wa)) . N
_Vba_ = (Vbi + Rb.GetCrossProductWith(Wbi) - Vai - Ra.GetCrossProductWith(Wai)).GetDotProductWith(N);
//If and only if bodies approach then simulate Fl64Vector3d NaxRa;
Fl64Vector3d NbxRb;
Fl64Vector3d NaaxRaa;
Fl64Vector3d NbbxRbb;
NaxRa.MakeCrossProductOf_OtherA_x_OtherB(N, Ra); //This is in the global frame
NbxRb.MakeCrossProductOf_OtherA_x_OtherB(-N, Rb); //This is in the global frame
//Correct NxR for the orientation of the rigid body
NaaxRaa.MakeRotationOf_OtherVector_TransposeAnyMatrix(NaxRa, Oa);
NbbxRbb.MakeRotationOf_OtherVector_TransposeAnyMatrix(NbxRb, Ob);
//Corrected H vectors
//Hx = (NyRz - NzRy)/rx
//Hy = (NzRx - NxRz)/ry
//Hz = (NxRy - NyRx)/rz
Fl64Vector3d Ha;
Fl64Vector3d Hb;
Ha[0] = NaaxRaa[0] / ra[0];
Ha[1] = NaaxRaa[1] / ra[1];
Ha[2] = NaaxRaa[2] / ra[2];
Hb[0] = NbbxRbb[0] / rb[0];
Hb[1] = NbbxRbb[1] / rb[1];
Hb[2] = NbbxRbb[2] / rb[2];
//Calculate the apparent mass
//_M_ = M / (1 + sqmod(H))
//double _Ma_;
//double _Mb_;
//_Ma_ = Ma / (1 + Ha.GetSquareMagnitude());
//_Mb_ = Mb / (1 + Hb.GetSquareMagnitude());
#define sqmod(H) (H.GetSquareMagnitude()) //Calculate Impulse in the direction from b to a
double Ja;
//Impulse = 2 * (_Vbi_ - _Vai_) / ((1 + sqmod(Hb))/Mb + (1 + sqmod(Ha))/Ma)
Ja = 2.0 * (_Vba_) / ((1 + sqmod(Hb))/Mb + (1 + sqmod(Ha))/Ma);
if(Ja < 0.0) goto START;//Just in case, only approaching bodies are used //Calculate the change in 'velocities'
dVa = (Ja / Ma) * N;
dVb = (Ja / Mb) * (-N);
//dWaa = J(NxR/I)
//Wx = ((NyRz - NzRy)J/ Ix)
//Wx = (Hx/rx) J/ M
Fl64Vector3d dWaa;
Fl64Vector3d dWbb;
dWaa[0] = (Ja / Ma) * (Ha[0]/ra[0]);
dWaa[1] = (Ja / Ma) * (Ha[1]/ra[1]);
dWaa[2] = (Ja / Ma) * (Ha[2]/ra[2]);
dWbb[0] = (Ja / Mb) * (Hb[0]/rb[0]);//Hb was calculated with minus N
dWbb[1] = (Ja / Mb) * (Hb[1]/rb[1]);
dWbb[2] = (Ja / Mb) * (Hb[2]/rb[2]);
dWa.MakeRotationOf_OtherVector_AnyMatrix(dWaa, Oa);
dWb.MakeRotationOf_OtherVector_AnyMatrix(dWbb, Ob);
//Calculate the final 'velocites'
Vaf = Vai + dVa;
Vbf = Vbi + dVb;
Waf = Wai + dWa;
Wbf = Wbi + dWb;
/*
Calculate the final angular and linear momentum
*/
// Energy
Fl64Vector3d Gaf; //Final linear momentum
Fl64Vector3d Gbf; //Final linear momentum
Fl64Vector3d Laf; //Final angular momentum
Fl64Vector3d Lbf; //Final angular momentum
CalculateAngularMomentum(Waf, Ia, Oa, Laf);
CalculateAngularMomentum(Wbf, Ib, Ob, Lbf);
CalculateLinearMomentum(Vaf, Ma, Gaf);
CalculateLinearMomentum(Vbf, Mb, Gbf);
/*
Calculate the final rotational and translational energy
*/
// Energy
double Etaf; //Final translational energy
double Eraf; //Final rotational energy
double Etbf; //Final translational energy
double Erbf; //Final rotational energy
CalculateRotationalEnergy(Waf, Ia, Oa, Eraf);
CalculateRotationalEnergy(Wbf, Ib, Ob, Erbf);
CalculateTranslationalEnergy(Vaf, Ma, Etaf);
CalculateTranslationalEnergy(Vbf, Mb, Etbf);
/*
Print the results
*/
//Approaching velocity
printf("\nApproaching velocity\t=\t%0.13f", _Vba_);
//Energy conservation
printf("\nEnergy before\t=\t%0.13f", Erai + Erbi + Etai + Etbi);
printf("\nEnergy after\t=\t%0.13f", Eraf + Erbf + Etaf + Etbf);
printf("\n");
printf("\nUsing the global axes\n");
//M and I and Orientation and R and N
printf("\nThe objects characteristics:\n");
printf("\nMasses of objects A and B");
printf("\nMa\t=\t%0.13f", Ma);
printf("\nMb\t=\t%0.13f", Mb);
printf("\n");
printf("\nInertia about principal axes for objects A and B");
printf("\nIa\t=\t%0.13f, %0.13f, %0.13f", Ia[0], Ia[1], Ia[2]);
printf("\nIb\t=\t%0.13f, %0.13f, %0.13f", Ib[0], Ib[1], Ib[2]);
printf("\n");
printf("\nOrientation given as axis angle Qaxis, Qangle");
printf("\nQaxisa\t=\t%0.13f, %0.13f, %0.13f", (Qa.GetNormal())[0], (Qa.GetNormal())[1], (Qa.GetNormal())[2]);
printf("\nQanglea\t=\t%0.13f", Qa.GetMagnitude());
printf("\nQaxisb\t=\t%0.13f, %0.13f, %0.13f", (Qb.GetNormal())[0], (Qb.GetNormal())[1], (Qb.GetNormal())[2]);
printf("\nQangleb\t=\t%0.13f", Qb.GetMagnitude());
printf("\n");
printf("\nThe vector from the center of mass to the collision point for A and B");
printf("\nRa\t=\t%0.13f, %0.13f, %0.13f", Ra[0], Ra[1], Ra[2]);
printf("\nRb\t=\t%0.13f, %0.13f, %0.13f", Rb[0], Rb[1], Rb[2]);
printf("\n");
printf("\nThe normal from B to A of the impulse");
printf("\nN\t=\t%0.13f, %0.13f, %0.13f", N[0], N[1], N[2]);
printf("\n");
printf("\nVai\t=\t%0.13f, %0.13f, %0.13f", Vai[0], Vai[1], Vai[2]);
printf("\nVaf\t=\t%0.13f, %0.13f, %0.13f", Vaf[0], Vaf[1], Vaf[2]);
printf("\n");
printf("\nVbi\t=\t%0.13f, %0.13f, %0.13f", Vbi[0], Vbi[1], Vbi[2]);
printf("\nVbf\t=\t%0.13f, %0.13f, %0.13f", Vbf[0], Vbf[1], Vbf[2]);
printf("\n");
printf("\nWai\t=\t%0.13f, %0.13f, %0.13f", Wai[0], Wai[1], Wai[2]);
printf("\nWaf\t=\t%0.13f, %0.13f, %0.13f", Waf[0], Waf[1], Waf[2]);
printf("\n");
printf("\nWbi\t=\t%0.13f, %0.13f, %0.13f", Wbi[0], Wbi[1], Wbi[2]);
printf("\nWbf\t=\t%0.13f, %0.13f, %0.13f", Wbf[0], Wbf[1], Wbf[2]);
printf("\n");
printf("\nLinear Momentum in X before\t=\t%0.13f", Gai[0] + Gbi[0]);
printf("\nLinear Momentum in X after\t=\t%0.13f", Gaf[0] + Gbf[0]);
printf("\nLinear Momentum in Y before\t=\t%0.13f", Gai[1] + Gbi[1]);
printf("\nLinear Momentum in Y after\t=\t%0.13f", Gaf[1] + Gbf[1]);
printf("\nLinear Momentum in Z before\t=\t%0.13f", Gai[2] + Gbi[2]);
printf("\nLinear Momentum in Z after\t=\t%0.13f", Gaf[2] + Gbf[2]);
printf("\n");
printf("\nAngular Momentum about X before\t=\t%0.13f", Lai[0] + Lbi[0]);
printf("\nAngular Momentum about X after\t=\t%0.13f", Laf[0] + Lbf[0]);
printf("\nAngular Momentum about Y before\t=\t%0.13f", Lai[1] + Lbi[1]);
printf("\nAngular Momentum about Y after\t=\t%0.13f", Laf[1] + Lbf[1]);
printf("\nAngular Momentum about Z before\t=\t%0.13f", Lai[2] + Lbi[2]);
printf("\nAngular Momentum about Z after\t=\t%0.13f", Laf[2] + Lbf[2]);
printf("\n");
//I am trying different methods of adding the angular momentum
printf("\nAngular Momentum Magnitude before\t=\t%0.13f", (Lai + Lbi).GetMagnitude());
printf("\nAngular Momentum Magnitude after\t=\t%0.13f", (Laf + Lbf).GetMagnitude());
printf("\n");
printf("\nAngular Momentum Using Local before\t=\t%0.13f", (Lai.GetMagnitude()) + (Lbi.GetMagnitude()));
printf("\nAngular Momentum Using Local after\t=\t%0.13f", (Laf.GetMagnitude()) + (Lbf.GetMagnitude()));
printf("\n");
printf("\nRotational Energy of A before\t=\t%0.13f", Erai);
printf("\nRotational Energy of A after\t=\t%0.13f", Eraf);
printf("\nRotational Energy of B before\t=\t%0.13f", Erbi);
printf("\nRotational Energy of B after\t=\t%0.13f", Erbf);
printf("\n");
printf("\nTranslational Energy of A before\t=\t%0.13f", Etai);
printf("\nTranslational Energy of A after\t=\t%0.13f", Etaf);
printf("\nTranslational Energy of B before\t=\t%0.13f", Etbi);
printf("\nTranslational Energy of B after\t=\t%0.13f", Etbf);
printf("\n");
printf("\nRotational Energy of A and B before\t=\t%0.13f", Erai + Erbi);
printf("\nRotational Energy of A and B after\t=\t%0.13f", Eraf + Erbf);
printf("\n");
printf("\nTranslational Energy of A and B before\t=\t%0.13f", Etai + Etbi);
printf("\nTranslational Energy of A and B after\t=\t%0.13f", Etaf + Etbf);
printf("\n");
printf("\n");
}
//END:
return 0;
}
|