Idris Examples
Vectors
In both the dependent sum type and the dependent product type examples below the type declaration has two terms where the second depends on the first. However the definition of the sum type requires a specific value wheras the definition of the product type applies to all possible values.
Dependent Sum Type (dependent pair) |
myvect : (n:Nat ** Vect n String)
myvect = (3 ** ("a", "b", "c") |
| Dependent Product Type | myvect : n:Nat -> (Vect n String) myvect n = 3 *n |
Implemetations of Dependent Product Type
Vect is an example of a type which depends on:
|
||| Vectors: Generic lists with explicit length in the type ||| @ len the length of the list ||| @ elem the type of elements data Vect : (len : Nat) -> (elem : Type) -> Type where ||| Empty vector Nil : Vect Z elem ||| A non-empty vector of length `S len`, consisting of ||| a head element and the rest of the list, of length `len`. (::) : (x : elem) -> (xs : Vect len elem) -> Vect (S len) elem |
So in this example we are saying that Vect exists for all types 'elem' and for all numbers 'len'.
Most programs that support this have a special notation for it.
So this is a product type where one of the types is a function (family of types).
| So instead of the usual product: | Pair A B | |
| we have : | DPair A (A -> Type) | |
| For example: | DPair Nat (Nat -> Type) | |
| There is a special notation in Idris: | A ** (A -> Type) |
Notation
 |
~> idris -p base Data/Vect.idr
/ _/___/ /____(_)____
/ // __ / ___/ / ___/ Version 1.3.2
_/ // /_/ / / / (__ ) http://www.idris-lang.org/
/___/\__,_/_/ /_/____/ Type :? for help
Idris is free software with ABSOLUTELY NO WARRANTY.
For details type :warranty.
*Data/Vect> (n : Nat ** Vect n String)
(n : Nat ** Vect n String) : Type
|
Example
In the introduction dependent types were introduced with the example of vect. |
specificVect : (n : Nat ** Vect n String) specificVect = (3 ** ["a","b","c"]) |
| We can also show dependent sum types using Vect. | *typeTheory> specificVect (3 ** ["a", "b", "c"]) : (n : Nat ** Vect n String) |
In the product case there was a type for every n which is represented by a function (n -> Vect n elem). In the sum case there is one type given by a single 'n' which is represented by a product/tuple (n ** Vect n elem) but because the second element of the tuple depends on the first '**' is used to seperate the elements instead of ','.
Example - Expressions
The aim here is to try to model the context of variable declarations (or of premises in logic) as an index.
| Start by creating a very simple expression type to work with. | ||| Expression over some type 't' data Expression t = Lit t Var String (+) (Expression t) (Expression t) |
| Now give it the ability to bind | ||| Expression which binds some variable 'v' data BindExpression t (v:String) = BoundVar v (Expression t) Nested v (BindExpression t v) |
I haven't yet worked this through.
Example - Variable Scope
Here we try to model the situation where we define variables and then use them either in the same block or in a sub block. So we need to determine which definition to use based on the scope.
How can we revers the arrows so that we can get back to a definition from a variable use?
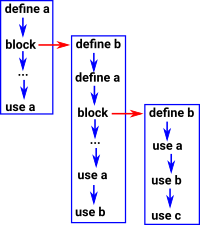 |
|
Implementation Code
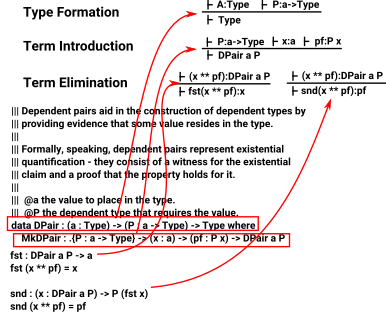
Idrisfrom : Idris-dev/libs/prelude/Builtins.idr |
||| Dependent pairs aid in the construction of dependent types by
||| providing evidence that some value resides in the type.
|||
||| Formally, speaking, dependent pairs represent existential
||| quantification - they consist of a witness for the existential
||| claim and a proof that the property holds for it.
|||
||| @a the value to place in the type.
||| @P the dependent type that requires the value.
data DPair : (a : Type) -> (P : a -> Type) -> Type where
MkDPair : .{P : a -> Type} -> (x : a) -> (pf : P x) -> DPair a P
|
Dependent Types in Programming
| In the language 'Scala' we can define a type that is parameterised by another type (polymorphism) for instance: | List[T] |
This represents a list of any type, represented by 'T', for example a list of Integers or a list of boolean values.
However, Scala does not allow dependent products like say: Modulo[n:Integer] which would represent any modulo number system such as modulo 3 or modulo 27.