Octonions are a superset of quaternions in the same way that quaternions are a superset of complex numbers. So,
- Scalars are represented by 1 number.
- Complex numbers are represented by 2 numbers (1 real and 1 imaginary).
- Quaternions are represented by 4 numbers (1 real and 3 imaginary).
- Octonions are represented by 8 numbers (1 real and 7 imaginary).
We might expect this sequence to continue with an element consisting of 16 numbers, but such an algebra does not exist, and the sequence ends with octonions. There are algebras, such as matrices and multivectors, which can have more than 8 dimensions but these don't have the same properties that division always exists and norms preserved by multiplication.
Soon after quaternions were discovered by Hamilton then octonions were discovered separately by John Graves and Arthur Cayley. Octonions are sometimes known as cayley numbers.
When we move from Complex numbers to Quaternions and then Octonions the system obeys fewer algebraic laws. When we go from Complex numbers to Quaternions we loose commutatively and when we go from Quaternions to Octonions we loose associatively.
Applications of Octonions
Octonions have been used in fields such as abstract algebra and topology but have not really made a big impact. In 1925 Wigner and John von Neumann tried and failed to make octonions the basis of quantum mechanics. More recently octonions have been used as the basis for String Theory so octonions may yet prove to be important in describing the structure of the universe.
Relationship to Group Theory
I don't really understand this, the definition of a group requires associatively so can octonions with the operation of multiplication be a group?
I have read that the exceptional groups (G2,F4,E6,E7 and E8) especially G2 are associated with octonions, how can that be??
Also the group SU2 is described as 2 complex dimensions and the group SU3 is described as 3 complex dimensions, these sound very similar to the definitions of quaternions and octonions, so is there any connection there?
Also can quaternion and octonion algebra be generated by Pauli Matricies?
Arithmetic of Octonions
With quaternions the imaginary terms were i, j and k. In the case of octonions we use e1, e2, e3, e4, e5, e6 and e7.
When adding octonions we just add the corresponding terms.
When multiplying octonions there are rules for combining the different imaginary operators. The square of any imaginary operator is -1. The multiplication rules can be shown by the 'fano plane':
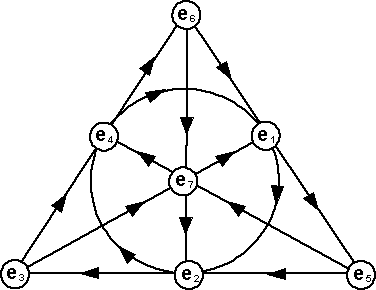
It works as follows, if you want to multiply e3 by e7 for example, look at the diagram and find the line that joins them and you will see that there is a third point on the line, in this case e1. Following the arrows, you go from e3 to e7 to e1 so e3 x e7 = e1reversing the order of the multiplicands gives minus the result so if the order on the line is reversed then put a negative sign in front of the result.
Multiplication table for octonions.
a*b |
b.1 | b.e1 | b.e2 | b.e3 | b.e4 | b.e5 | b.e6 | b.e7 |
| a.1 | 1 | e1 | e2 | e3 | e4 | e5 | e6 | e7 |
| a.e1 | e1 | -1 | e4 | e7 | -e2 | e6 | -e5 | -e3 |
| a.e2 | e2 | -e4 | -1 | e5 | e1 | -e3 | e7 | -e6 |
| a.e3 | e3 | -e7 | -e5 | -1 | e6 | e2 | -e4 | e1 |
| a.e4 | e4 | e2 | -e1 | -e6 | -1 | e7 | e3 | -e5 |
| a.e5 | e5 | -e6 | e3 | -e2 | -e7 | -1 | e1 | e4 |
| a.e6 | e6 | e5 | -e7 | e4 | -e3 | -e1 | -1 | e2 |
| a.e7 | e7 | e3 | e6 | -e1 | e5 | -e4 | -e2 | -1 |
The above table does not seem to have any pattern and it does not appear to be a superset of quaternions. However we can generate an equivalent table by swapping rows and columns as described on this page. We can get the properties we want by swapping e7 & e2 then e4 & e6 then e6 & e7. (note when we swap we must do the same thing to rows, columns and all entries.
Table for: octonion
| a*b | b.1 | b.i | b.j | b.k | b.l | b.li | b.lj | b.lk |
| a.1 | 1 | i | j | k | l | li | lj | lk |
| a.i | i | -1 | k | -j | li | -l | -lk | lj |
| a.j | j | -k | -1 | i | lj | lk | -l | -li |
| a.k | k | j | -i | -1 | lk | -lj | li | -l |
| a.l | l | -li | -lj | -lk | -1 | i | j | k |
| a.li | li | l | -lk | lj | -i | -1 | -k | j |
| a.lj | lj | lk | l | -li | -j | k | -1 | -i |
| a.lk | lk | -lj | li | l | -k | -j | i | -1 |
analysing commutivity: table does not commute: for example: i*j != j*i
analysing associativity: table does not associate, for example, (i* j)* l=k* l=lk is not equal to i*(j* l)=i*lj=-lk
how these results were generated.
As the above link explains, the table was generated by a computer program using a modification of Cayley-Dickson process.
Relationship to multivectors.
What is the relationship between octonions and multivectors (elements of Clifford or Geometric algebra. This topic is discussed on this page.
Pauli matrices
I'm not sure that octonions can be represented by pauli matricies since octonions are not associative and matricies are associative (assuming the elements of the matricies are associative).
Could octonions be related in some way to 4D rotations, if that were the case can we find some way to relate octonions to the following generators:
For 4D rotations (SU(3) group) the generators are:
|
|
|
|
|
|
|
|

