This is about how we measure the position on the surface of the earth, or possibly another planet.
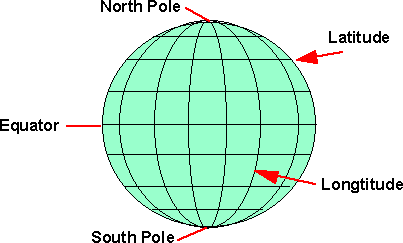
If we start by making an assumption that the earth is a perfect sphere, in this case we can use Spherical Polar Coordinates, as defined on this page. We can define a position on the earth using two angles:
- Latitude - an angle which is +90 degrees at the north pole, 0 degrees at the equator and -90 degrees at the south pole.
- Longitude - an angle about the line between the north and south poles, with 0 degrees at the Greenwich meridian.
We can assign an arbitrary x,y,z coordinate system in the local frame of the earth:
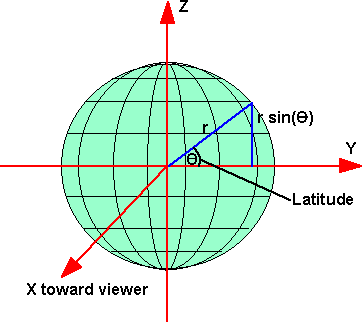
so from this diagram we can see that:
z = r sin(latitude)
and if we are on the Greenwich meridian then:
x = r cos(latitude)
but if we are not on the Greenwich meridian then this has to be modified depending on the latitude, so,
x = r cos(latitude) cos (longitude)
the y can be calculated from:
r2 = x2 + y2 + z2
therefore y = r *sqrt(1 - sin(latitude) - cos(latitude) cos (longitude))
where:
r = radius of the earth (approx. 6378135 metres)
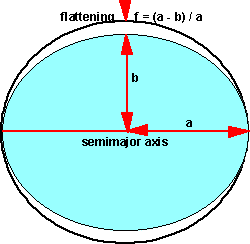
Ellipsoid
The earth is not quite spherical, it is slightly flattened at the poles relative to the equator, this shape is known as an ellipsoid. This is a closer approximation, but not perfect, so many ellipsoids have been defined for different regions of the world.
Earth ellipsoids supported by x3d
| x3d Code | Ellipsoid Name | a - Equatorial Radius (metres) | f - Flattening |
|
AA
|
Airy 1830 | 6377563.396 | 1/299.3249646 |
|
AM
|
Modified Airy | 6377340.189 | 1/299.3249646 |
|
AN
|
Australian National | 6378160 | 1/298.25 |
|
BN
|
Bessel 1841 (Namibia) | 6377483.865 | 1/299.1528128 |
|
BR
|
Bessel 1841 (Ethiopia Indonesia...) | 6377397.155 | 1/299.1528128 |
|
CC
|
Clarke 1866 | 6378206.4 | 1/294.9786982 |
|
CD
|
Clarke 1880 | 6378249.145 | 1/293.465 |
|
EA
|
Everest (India 1830) | 6377276.345 | 1/300.8017 |
|
EB
|
Everest (Sabah & Sarawak) | 6377298.556 | 1/300.8017 |
|
EC
|
Everest (India 1956) | 6377301.243 | 1/300.8017 |
|
ED
|
Everest (W. Malaysia 1969) | 6377295.664 | 1/300.8017 |
|
EE
|
Everest (W. Malaysia & Singapore 1948) | 6377304.063 | 1/300.8017 |
|
EF
|
Everest (Pakistan) | 6377309.613 | 1/300.8017 |
|
FA
|
Modified Fischer 1960 | 6378155 | 1/298.3 |
|
HE
|
Helmert 1906 | 6378200 | 1/298.3 |
|
HO
|
Hough 1960 | 6378270 | 1/297 |
|
ID
|
Indonesian 1974 | 6378160 | 1/298.247 |
|
IN
|
International 1924 | 6378388 | 1/297 |
|
KA
|
Krassovsky 1940 | 6378245 | 1/298.3 |
|
RF
|
Geodetic Reference System 1980 (GRS 80) | 6378137 | 1/298.257222101 |
|
SA
|
South American 1969 | 6378160 | 1/298.25 |
|
WD
|
WGS 72 | 6378135 | 1/298.26 |
|
WE
|
WGS 84 | 6378137 | 1/298.257223563 |
We can assign an arbitrary x,y,z coordinate system in the local frame of the
earth:

so from this diagram we can see that:
z = a * (1 -f) *sin(latitude)
and if we are on the Greenwich meridian then:
x = a cos(latitude)
but if we are not on the Greenwich meridian then this has to be modified depending on the latitude, so,
x = a cos(latitude) cos (longitude)
the y can be calculated from:
r2 = x2 + y2 + z2
therefore y = a *sqrt(1 - (1 -f) *sin(latitude) - cos(latitude) cos (longitude))
where:
- a = radius (on semimajor axis) of the earth
- f = flattening = (a - b) / a
