Steering works because it is easy for the wheel to move perpendicular to its axis but hard for it to move parallel to its axis. Therefore the car tends to turn in the direction that the wheels are pointed.
When the front wheels are turned the component of force in the direction of the wheel has very little reaction but the component normal to the wheel has a high reaction because the wheel cant turn in that direction.

Turning Radius
One way to define the amount of cornering that the car is making might be the angle of the wheels, marked as theta in the diagram. However, a more useful measure might be the turning radius, this has less dependancy on the geometry of the car, but it has the disadvantage that when the car is travelling in a straight line the turning radius is infinity. It might therefore be better to store it as 1/r.
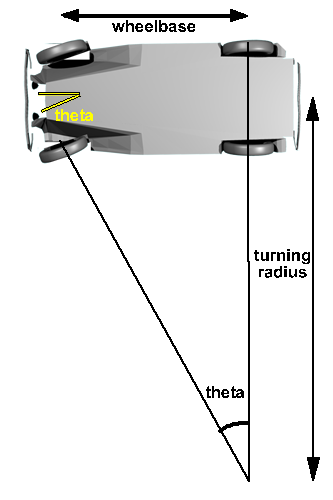
These are related as follows:
tan(theta) = wheelbase/turning radius
This is equivalent to an acceleration towards the centre of the turning circle.
a = v2/r
where:
- a = centripedal acceleration
- v = linear velocity of car
- r = turning radius
In the frame of reference of the car this appears as a 'centripedal force' pushing the car and its occupents outward. In the inertial frame of reference this is just the mass trying to go in a straight line rather than a different type of force. However, when modelling the game, it may be useful to work in the frame of reference of the car. Therefore the centripedal force is a useful fiction.
So how do we represent the status of the car, in the program, so far? That is, the values that might possibly change in every frame, I think we need to hold the following structure:
public class carStatus {
vector2d s // position of the centre of mass, integral of v,
vector2d v // velocity, integral of a, relative to orientation (along wheels, skid)
vector2d a // acceleration, depends only on forces acting at the time (along wheels, skid).
complex orientation // normalised complex number giving orientation of car (direction of front)
double ir // 1/r inverse of turning radius
}
Using complex numbers to represent orientations is discussed on this page. I would like to investigate using dual complex nubers to link orientation and position as discussed on this page.
Forces & Torques - Cornering
The reaction of the road is not inline with the Inertia (centrifical force) this produces a turning moment which tends to rotate the car. If it is high enough the car could be on two wheels.

This site may have errors. Don't use for critical systems.



