Why XSemantics?
The XSemantics website on Souceforge describes XSemantics like this:
"XSemantics is a DSL (implemented in Xtext itself) for writing type systems, reduction rules, interpreters (and in general relation rules) for languages implemented in Xtext. It then generates Java code that can be used in your language implemented in Xtext for scoping and validation (it can also generate a validator in Java)."
After reading this it is still not entirely clear to me exactly what XSemantics is, however, looking at the examples I can see that it is very powerful and potentially very useful.
It does not help that (to quote from the documentation) "XSemantics is thought to be used by people who are at least a little familiar with formal type systems and operational semantics". This appears to limit the potential users of what looks like useful software.
When I look at XSemantics it seems to me that it might be explainable to a wider audience as a rule based system, but we might expect rules to have the form:
if some predicate then some conclusion
like this:
| if | the current node is NumberLiteral | then | the current node is of type IntType. |
| Which in XSemantics is written: |
|
Another example is:
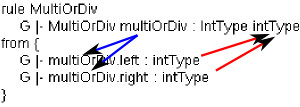
| if | the current node is MultiOrDiv and left is intType and right is intType | then | the current node is of type IntType. |
| Which in XSemantics is written: |
|
As far as I can see, it appears to be doing a pattern search on the rule: G |- MultiOrDiv to check if this is a MultiOrDiv node, if so, multiOrDiv holds this instance. Then all the conditions in the from part are checked. If they are all true then the right hand part of the rule is returned. |
 |
Relationship to Mathematical Logic and Type Theory
Since XSemantics uses mathematical logic it might be useful to try to describe the above in these terms.
If we have the situation where, if A is true and B is true then A/\B is true, the usual notation is shown on the right: |
|
We may require that this is only true in a certain context, to emphasise this in a more precise way we can write: |
|
More on these pages:
Installing XSemantics
For information about installing XSemantics see page here.
