SPAD allows symbolic expressions to be created, this uses the Expression domain which in turn uses the Kernel domain. Expression has specific support for symbolic expressions in terms of domains/categories (such as: GcdDomain, Integer, IntegralDomain, Ring, AbelianMonoid and SemiGroup). That is the code has specific tests and chunks of code for these. Symbolic functions are explicitly listed in Expression (such as: pi, exp, log, sin, cos...).
This is very powerful for algebras, like 'ring' and 'field' that are well supported. What I would like to do is allow symbolic expressions to be created and manipulated (for example equation solvers where this is possible) for any domain I am working on. Just to make this clear, SPAD already allows a value of any type to be given an alphanumeric label, we can set this to a value given by an expression but this must always evaluate to a literal value. We can't, in general, put an unknown on the right hand side of an assignment. I would like better general support for equations and equation solvers for any domain. Also I would like to be able to express (and preferably to enforce) the axioms for a given domain.
For example, I would like to have symbolic names for elements of a Clifford algebra and to be able to create expressions involving these. I would like to be able to do this without hacking the Expression domain (which is already very messy). It would be much better for people working on the code if this were done in, or near, the Clifford algebra domain. I would not want to duplicate the general expression handling code, only separate out the parts that change for different algebras.
This may not be simple so, on this page, I would like to try to discover the top level principles.
Variables verses Combinators
I can think of two ways to approach the above issues:
- To allow expressions which contain 'unknowns' which are represented by symbols.
- To use combinators.
In the first we would need to have 'equations'. SPAD supports equations (in 'Equation' domain) but, again, it does not seem general in that it is based on predefined operations like: +,-,*,/,1 and = so it has to have specific code for various categories of algebras. The Equation domain also has support for specific operations on the whole equation such as differentiation.
The Equation domain has a representation containing lhs and rhs both of which can be any type.
Combinators could use a language like 'Joy' which is based on the concept of a stack.
Catamorphism and Anamorphism
| If we start with an algebra that has a binary operation (S,S)->S and, instead of supplying interal values we supply a symbolic value to represent a variable or unknown, we might build up a free algebra. |  |

- Catamorphism - initial algebra -> other algebra.
- Anamorphism
Catamorphism
Reduces the data structure to a required value.
Tree is a initial object in the category of F-algebras
Anamorphism
Upwards morphism - Builds an invocation tree as an explicit data structure.
zip and iterate are examples of anamorphisms
A notation for ana(f) found in the literature is [(f)]. The brackets used are known as lens brackets.
Hylomorphism
Composition of an anamorphism and a catamorphism. Invocation tree is isomorphic to a function which processes lists.
Example Monoid
free monoid = list
- Fold is a catamorphism
- Unfold is a anamorphism
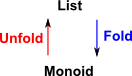
| Fold Left | 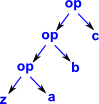 |
| Fold Right | 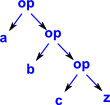 |
So the fold operation takes a list and a monoid and returns a value
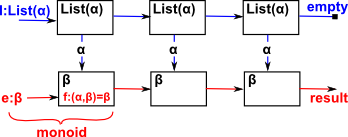
Googles MapReduce software framework.
Example Field
free field = tree?

Monoid and Monad
| Monoid | Monad | |
|---|---|---|
| Definition | A set: S An operation: •: S×S->S An element of S: e:1->S |
an endofunctor: T natural transformations: multiplication µ: T×T-> T unit η: 1->T |
| Satisfies Laws | (a•b)•c=a•(b•c) e•a=a=a•e for all a,b,c |
µ(µ(T×T)×T)=µ(T×µ(T×T)) µ(η(T)) = T = T(η) |
Algebraic Category
Every Algebraic Category has co-limits
The category Alg T is a free completion of Top under sifted colimits