Maths - Quaternion Arithmetic - Other approaches

The multiplication rules for the imaginary operators are the same as for other numbers. We just put each quaternion in brackets and multiply out all the terms: (a + i b + j c + k d)*(e + i f + j g + k h). When we are multiplying the imaginary operators we use the following rules:

• i*i = j*j = k*k = -1
• i*j = k,
• j*i = -k
• j*k = i,
• k*j = -i
• k*i = j,
• i*k = -j

Note that the order of multiplication is significant, in other words q1 * q2 is not necessarily equal to q2 * q1, we might expect this because quaternions can be used to represent rotations and the order of rotations is significant, for example, if you rotate 90 degrees about the x-axis and then 90 degrees about the y-axis you get a different result than if you rotate about the y-axis then the x-axis. See here for more information about the rules of rotation.

In mathematical terms quaternion rotation is not necessarily commutative, some subsets of quaternions may commute, for example:

• real part: a*e = e*a
• real times imaginary: a * i f = i f * a
• same imaginary part: i b * i f = i f * i b ( = -b*f )

Other subsets of quaternions anti-commute, in other words reversing the order multiplies the result by -1. This apples when different imaginary quantities, as can be seen from the list above, so for example:

• i*j = - j*i = k

In the general case quaternions containing all these parts would be neither commutative nor anti-commutative. In order to understand more about the effect of reversing the operands it is useful to introduce the concept of the conjugate explained here. If the quaternion is unit length (normalised) as when used to represent rotations:

conj(q1 * q2) = conj(q2) * conj(q1)

In other words, to reverse the order, take the conjugate of each part and then take the conjugate of the whole thing.

So for the general case just expand out the terms and group as follows:

(a + i b + j c + k d)*(e + i f + j g + k h)	=a(e + i f + j g + k h) + i b(e + i f + j g + k h) + j c(e + i f + j g + k h) + k d(e + i f + j g + k h)
=	a*e + i a*f + j a*g + k a*h + i b*e + i*i * b*f + i*j * b*g + i*k * b*h + j c*e + j*i * c*f + j*j * c*g + j*k * c*h + k d*e + k*i * d*f + k*j * d*g + k*k * d*h
=	a*e + i a*f + j a*g + k a*h + i b*e - b*f + k * b*g -j * b*h + j c*e - k * c*f - c*g + i * c*h + k d*e + j * d*f -i * d*g - d*h
=	a*e - b*f - c*g - d*h + i (b*e + a*f + c*h- d*g) + j (a*g - b*h+ c*e + d*f) + k (a*h + b*g - c*f + d*e)

so the result is:

z1 * z2= a*e - b*f - c*g- d*h + i (b*e + a*f + c*h - d*g) + j (a*g - b*h + c*e + d*f) + k (a*h + b*g - c*f + d*e)

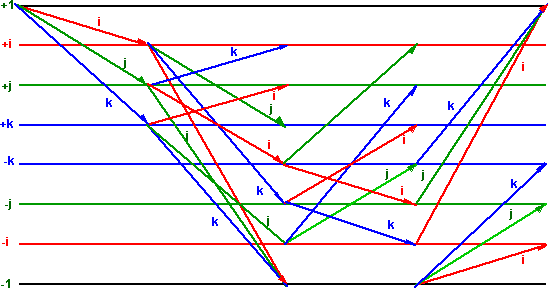
I have tried to show all the possible transitions for multiplications by the unit vectors in the following diagram: