This is a continuation of the tutorial for the graph theory code which starts here. If you have not already installed and loaded the code from 'graph.spad' then you first need to follow the instructions on that page.
This graph framework has many methods to create graph instances such as:
- Constructing graphs by building up individual objects and arrows.
- Constructing from adjacency matrix.
- Constructing standard types.
- Combining existing graphs using sum and product.
- Mapping from an existing graph.
- Constructing from permutation.
We will construct our graphs over 'String'. If you don't care what the graph is constructed over, then 'String' is a good choice, as it allows us to use the string to name the nodes.
Constructing graphs by building up individual objects and arrows.
In (2) we create a minimal graph with 2 vertices "a" and "b" and no arrows between them.
We can add additional vertices using 'addObject!' as in (3)
And we can add arrows as in (4) and (5)
(1) ->GS := DirectedGraph(String)
(1) DirectedGraph(String)
Type: Type
(2) ->hs := directedGraph(["a","b"])$GS
(2) "a,b"
Type: DirectedGraph(String)
(3) ->addObject!(hs,"c")$GS
(3) "a,b,c"
Type: DirectedGraph(String)
(4) ->addArrow!(hs,"alpha",1,2)
(4) "a,b,c|alpha:a->b"
Type: DirectedGraph(String)
(5) ->addArrow!(hs,"alpha",2,3)
(5) "a,b,c|alpha:a->b,alpha:b->c"
Type: DirectedGraph(String)
|
The graph generated so far does not have any information to help us draw it out. If we want to tell it the position of the vertices we have to construct it in a slightly different way. Now create graph suitable for diagram:
(6) -> OBJT ==> Record(value:String,posX:NNI,posY:NNI)
Type: Void
(7) -> oba:OBJT := ["a",10,10]
(7) [value= "a",posX= 10,posY= 10]
Type: Record(value: String,posX: NonNegativeInteger,posY: NonNegativeInteger)
(8) -> obb:OBJT := ["b",10,60]
(8) [value= "b",posX= 10,posY= 60]
Type: Record(value: String,posX: NonNegativeInteger,posY: NonNegativeInteger)
(9) -> obc:OBJT := ["c",60,10]
(9) [value= "c",posX= 60,posY= 10]
Type: Record(value: String,posX: NonNegativeInteger,posY: NonNegativeInteger)
(10) -> hs2 := directedGraph([oba,obb,obc])$GS
(10) "a,b,c"
Type: DirectedGraph(String)
(11) -> addArrow!(hs2,"alpha",1,2)$GS
(11) "a,b,c|alpha:a->b"
Type: DirectedGraph(String)
(12) -> addArrow!(hs2,"beta",2,3)$GS
(12) "a,b,c|alpha:a->b,beta:b->c"
Type: DirectedGraph(String)
(13) -> diagramSvg("testGraph2s1.svg",hs2,true)
Type: Void |
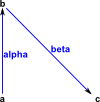 |
We can edit the diagram by using a program such as Inkscape. This may be necessary to tidy things up, stop symbols overlapping an so on. |
Constructing from adjacency matrix.
We can also construct a graph with given objects and adjacency matrix.
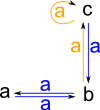 |
(14) -> hs2 := directedGraph(["a","b","c"],_
[[0::NNI,1::NNI,0::NNI],_
[1::NNI,0::NNI,1::NNI],_
[0::NNI,1::NNI,1::NNI]])$GS
(14) "a,b,c|a:a->b,a:b->a,a:b->c,a:c->b,a:c->c"
Type: DirectedGraph(String)
(15) -> diagramSvg("testGraph2s2.svg",hs2,true)
Type: Void |
For information about adjacency matrix see this page.
Constructing standard types.
In the same way that other algebras have special elements like "0" and "1" there are special elements in Graph which we can construct as follows:
The terminal graph consists of a single vertex and a single arrow. It always has a unique map to it from any other graph.
(16) -> T := terminal("a")$GS
(16) "a|loop:a->a"
Type: DirectedGraph(String) |
The initial graph has no vertices or arrows and always has a unique map from it to any other graph.
(17) -> I := initial()$GS
(17) ""
Type: DirectedGraph(String) |
In addition to these special elements we have a number of 'standard graphs', these contain any number of specified objects connected in the pattern described. The Wiki page here lists named graphs such as:
- Complete graphs
- Complete bipartite graphs
- Cycles
- Friendship graphs
- Fullerene graphs
- Platonic solids
- Snarks
- Star
- Wheel graphs
- and so on....
So far this code only supports a few named types as follows:
Cycle
Usually denoted Cn where 'n' is the number of elements in the cycle.
cycleOpen(objs:List S,arrowName:String):% constructs a graph with objects given connected in a cycle but with one gap.
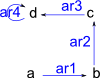 |
(18) -> G1 := cycleOpen(["a","b","c","d"],"ar")$GS
(18) "a,b,c,d|ar1:a->b,ar2:b->c,ar3:c->d,ar4:d->d"
Type: DirectedGraph(String)
(19) -> diagramSvg("testGraph2s3.svg",G1,true)
Type: Void |
'cycleClosed' constructs a graph with objects given connected in a cycle. That is a single loop containing all vertices.
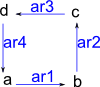 |
(20) -> G2 := cycleClosed(["a","b","c","d"],"ar")$GS
(20) "a,b,c,d|ar1:a->b,ar2:b->c,ar3:c->d,ar4:d->a"
Type: DirectedGraph(String)
(21) -> diagramSvg("testGraph2s4.svg",G2,true)
Type: Void |
Unit
'unit(objs:List S,arrowName:String):% constructs a graph with objects given and arrows from each object only to itself.
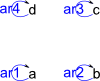 |
(22) -> G3 := unit(["a","b","c","d"],"ar")$GS
(22) "a,b,c,d|ar1:a->a,ar2:b->b,ar3:c->c,ar4:d->d"
Type: DirectedGraph(String)
(23) -> diagramSvg("testGraph2s5.svg",G3,true)
Type: Void |
Complete
Usually denoted Kn, where 'n' is the number of elements and K from German word komplett.
'kgraph' constructs a graph with objects given and fully connected arrows, that is, each object has an arrow to every other object except itself.
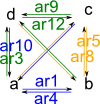 |
(24) -> G4 := kgraph(["a","b","c","d"],"ar")$GS
(24)
"a,b,c,d|ar1:a->b,ar2:a->c,ar3:a->d,ar4:b->a,ar5:b->c,
ar6:b->d,ar7:c->a,ar8:c->b,ar9:c->d,ar10:d->a,ar11:d->b,
ar12:d->c"
Type: DirectedGraph(String)
(25) -> diagramSvg("testGraph2s6.svg",G4,true)
Type: Void |
Constructing From Permutation
We can construct a graph from a list of permutations. Note, this is not a Cayley graph, it is a graph representing a set of permutations.
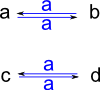 |
(26) -> cy := cycles([["a","b"],["c","d"]])
(26) ("a" "b")("c" "d")
Type: Permutation(String)
(27) -> G5 := directedGraph([cy])$GS
(27) "c,d,b,a|a:c->d,a:d->c,a:b->a,a:a->b"
Type: DirectedGraph(String)
(28) -> diagramSvg("testGraph2s7.svg",G5,true)
Type: Void |
We can also create a graph from a PermutationGroup, again the graph will represent a set of permutations, not a Cayley graph.
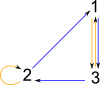 |
(29) -> dg2 := dihedralGroup(3)
(29) <(1 2 3),(1 3)>
Type: PermutationGroup(Integer)
(30) -> G6 := dg2::DirectedGraph(Integer)
(30) "2,3,1|a:2->1,a:2->2,a:3->2,a:3->1,a:1->3,a:1->3"
Type: DirectedGraph(Integer)
(31) -> diagramSvg("testGraph2s8.svg",G6,false)
Type: Void |
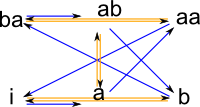
To get a true Cayley graph we must use the 'toCayleyGraph' function:
 |
(32) -> MF1 := MultifunctionGraph(Integer)
(32) MultifunctionGraph(Integer)
Type: Type
(33) -> CG := toCayleyGraph(dg2)$MF1
(33)
"i,a,b,aa,ab,ba|11:i->a,12:i->b,21:a->aa,22:a->ab,
31:b->ba,32:b->i,41:aa->i,42:aa->ba,51:ab->b,
52:ab->a,61:ba->ab,62:ba->aa"
Type: MultifunctionGraph(String)
(34) -> diagramSvg("testGraph2s9.svg",CG,false)
Type: Void |
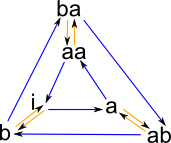 |
This Cayley graph may not be arranged in the most readable way but, since we have stored it in a SVG file, we can edit it, using Inkscape, by hand to get a more recognisable form like that on the left. |
That concludes our overview of ways to construct graphs, click here to go to the next stage of the tutorial which is about ways to view and investigate the various graphs.