See also topos theory.
The relationship X
I (X is a subset of I) is a predicate. We can form a category of predicates on sets as follows:
| Objects | predicates are pairs (I,X) where X(i) implies an element i |
 |
| Morphisms | (I,X) -> (J,Y) where: u:I-> J and X(i) implies: Y(u(i)) So, to define(I,X) -> (J,Y) , we need maps u:I -> J and X -> Y but X -> Y is implied by u. |
 |
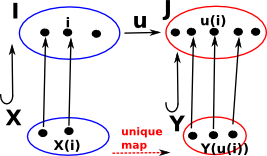Reverse map 'subsitution functor' u* |
examples of substitution are:
|
 |
| weakening |  |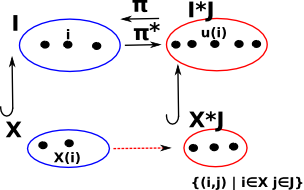
|
| contraction |  |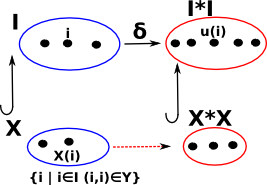
|
| quantifiers |  |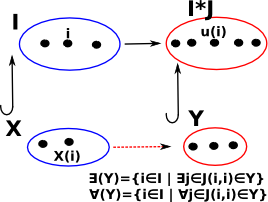
I is a free variable in I.