Isabelle Language

Top Level Strutcure

theory fileName
imports Main Datatype
begin

end

Definitions

This is the program-like. Similar to data and functions on that data.

The keyword 'primrec' is used for a certain type of 'primative recursion' where each recursive call peels off a datatype constructor from one of the arguments.

Notation

• 'a = type variable

Eamples of 'datatype'

• datatype bool = True | False
• datatype nat = 0 | Suc nat
• datatype 'a list = Nil | Cons 'a " 'a list"

fun

fun defines a function by pattern matching over datatype constructors.

Examples of 'fun'

• fun conj :: "bool => bool => bool" where
  "conj True True = True" |
  "conj _ _ = False"
• fun add :: "nat => nat => nat" where
  "add 0 n = n" |
  "add (Suc m) n = Suc (add m n)"

definiton

A definiton defines a non-recursive function without any pattern matching

Examples of 'definiton'

• definition sq :: "nat => nat" where
  "sq n = n n"

Abbreviations

Abbreviations have the same form as definitons but are only synthetic sugar.

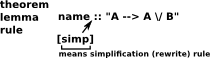
Theorems, Lemmas and Rules

Theorems, Lemmas and Rules are the same to the program. The difference is only intended to express the importance.

Proofs

apply(auto)
apply(simp name: theory1 theory2)
apply(force
apply(fastforce
apply(blast
sledgehammer
try

• done tells Isabelle to associate the lemma just proved with its name
• thm name - displays the theorem

Examples of Proofs

• lemma add_02: "add m 0 =m"
  apply (induction m)
  apply(auto)
  done

Results

The results show the proof state. The numbered lines are known as subgoals.

The prefix Vm: is Isabelle’s way of saying "for an arbitrary but fixed m". Universal quantifier at the meta level

The ==> separates assumptions from the conclusion.

Meta Level

Examples

theory Mylist
imports Datatype
begin

datatype 'a list = Nil ("[]")
                 | Cons 'a "'a list" (infixr "#" 65)

(* this is the append function: *)
primrec app :: "'a list => 'a list =>'a list" (infixr "@" 65)
where
"[] @ ys = ys" |
"(x # xs) @ ys = x # (xs @ ys)"

primrec rev :: "'a list => 'a list"
where
"rev []   = []" |
"rev (x # xs) = (rev xs) @ (x # [])"

value "rev (True # False # [])"
value "rev (c # b # a # [])"

theorem rev_rev [simp]: "rev (rev xs) = xs"
apply (induct_tac xs)
end

theory Test1
imports Main
begin
theorem A: "A \<longrightarrow> A \<or> B"
apply (rule impI)
apply (auto)
done

theorem B: "A \<or> B --> B \<or> A"
(*apply (rule impI)*)
apply (rule disjE)
apply (rule disjI2)
 apply (auto)
(*apply (rule disjI1)
 apply (auto) *)
done
end

Isar

proof ::= 'proof' method statement* 'qed'
         | 'by' method
statement ::= 'fix' variable+
         | 'assume' proposition+
         | ('from' fact+)? 'have' proposition+ proof
         | ('from' fact+)? 'show' proposition+ proof
proposition ::= (label':')? string
fact ::= label
method ::= '-' | 'this' | 'rule' fact | 'simp' | 'blast' | 'auto'
         | 'induct' variable | ...

• show statement establishes the conclusion of the proof
• have statement is for establishing intermediate results

shortcuts

• 'this' refers to the fact proved by the previous statement.
• 'then' = 'from this'
• 'hence' = 'then have'
• 'thus' = 'then show'
• 'with' fact+ = 'from' fact+ 'and' 'this'
• '.' = 'by this'
• '..' = 'by' rule where Isabelle guesses the rule

EuclideanSpace

home