When doing proofs about equations we sometimes need to replace a variable, that occurs in an equation, with some expression. For example, if we are working with natural numbers we may want to replace a vaiable 'k' with say '(S m)' everywhere it occurs in an equation.
The replace and rewrite functions allow us to substitute identical terms in an equation. For instance if:
'x=x+0' and 'y=x'
then
'y=y+0'
However Idris does not solve symultanous equations (a variable name inside some equation is not linked to the same name in other equations), instead Idris uses the indiscernability of identicals principle.
Indiscernability of Identicals
For any x and y, if x is identical to y, then x and y have all the same properties.
![]() x
x![]() y [ x = y ->
y [ x = y ->![]() P ( P x ↔ P y)]
P ( P x ↔ P y)]
Here these properties are usually equations.
|
Indiscernability of identicals doesn't entail reflexivity of = but both properties together entail symmetry and transitivity. Therefore, indiscernability of identicals and reflexivity is sometimes used as a (second-order) axiomatization for the equality relation. |
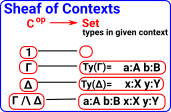
Properties

| In set theory a property can be given by a function from Set to Bool. For instace: the property of being an even number can be represented like this: | 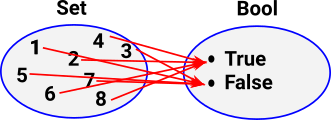 |
| Since we are using constructive logic we represent properties as a function into a type (in this case an equation). | 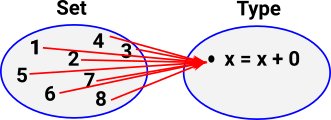 |
So, in Idris, this is not intended for a property like this: which can't be proved for all values of n (that is, it generates a type that can't be constructed, using Refl, for all values of n). |
p1: Nat -> Type p1 n = (n=2) |
|
Whereas a property like this: can be proved for all values of n |
p2: Nat -> Type p2 n = (n=n+0) |
| So 'p1' can be contructed at 2 but when we try to construct at 3 we get an error as expected: | *proof> the (p1 2) Refl
Refl : 2 = 2
*proof> the (p1 3) Refl
(input):1:1-15:When checking argument value to function Prelude.Basics.the:
Type mismatch between
x = x (Type of Refl)
and
p1 3 (Expected type)
Specifically:
Type mismatch between
1
and
0
|
| As expected we can construct 'p2' at any value. However this needs to be proved and, for this we need Replace or Rewrite. | *proof> the (p2 2) Refl Refl : 2 = 2 *proof> the (p2 3) Refl Refl : 3 = 3 *proof> |
Variables
We can represent variables in an equation by using dependent types, like this:
plusZeroRightNeutral: (x:Nat) -> (x = plus x Z)
So this generates a family of types:
- 0 = plus 0 Z
- 1 = plus 1 Z
- 2 = plus 2 Z
- ...
To prove it we must be able to construct for every value of x (it must be total).
An Example
The simplest example I can find is a proof that x=x+0 for all x.
total plusZeroRightNeutral : (x : Nat) -> (plus x Z) = x plusZeroRightNeutral Z = Refl plusZeroRightNeutral (S n) = rewrite (plusZeroRightNeutral n) in Refl |
Using cong
It is possible to prove this by using cong
total plusZeroRightNeutralC : (x : Nat) -> (plus x Z) = x
plusZeroRightNeutralC Z = Refl
plusZeroRightNeutralC (S n) = cong {f = S} (plusZeroRightNeutralC n) |
So (plusZeroRightNeutralC n) has type (plus x Z) = x that can be interpeted as,
(plusZeroRightNeutralC n) is a proof (that is a constructor) of (plus x Z) = x
'cong' is applied to this which says if we have a proof of (plus x Z) = x then we get a proof of S (plus x Z) = S x
So,
- cong {f = S} (plusZeroRightNeutralC n) is a proof (constuctor) of
(plus x Z) = x - (plusZeroRightNeutralC n) is a proof (constuctor) of
(plus n Z) = n
but x = S n so,
????
So 'cong' works for this case since we only need to apply the same function to both sides of the equation. In more complicated cases we may need to substitute variables so its worth using this example with replace/rewrite to gain understanding before we go on to more complex examples.
- Leibniz equality
- Leibniz characterized the notion of equality as follows:
- Given any x and y, x = y if and only if, given any predicate P, P(x) if and only if P(y).
- https://jesper.sikanda.be/files/leibniz-equality.pdf
- Heterogeneous equality
- 'John Major equality'
- http://adam.chlipala.net/cpdt/html/Equality.html#lab66
- Identity of indiscernibles
Replace
prop : (x : Nat) -> Type
prop x = (plus x Z) = x
total plusZeroRightNeutralRep : (x : Nat) -> (plus x Z) = x
plusZeroRightNeutralRep Z = Refl
plusZeroRightNeutralRep {x} (S n) =
replace {P = prop} (the (x = (S n)) Refl) plusZeroRightNeutralRep n |
| For the second case we need to proove that: if it is true for (S x) then its also true for 'x'. |
The following are extracts from a reply to a question I had on the Idris group, I need to think about these issues before I write it up:
Your goal for this whole expression on the RHS is to show that S (plus n 0) = S n
So you could write this line as plusZeroRightNeutral (S n) = cong $ plusZeroRightNeutral n, OK, I was trying to get from a proof of (plus n 0) = n to a proof of (plus (S n) 0) = S n because that seemed to be whats required for induction. |
plusZeroRightNeutral (S n) =
let inductiveHypothesis = plusZeroRightNeutral n in ?foo
and then call ":prove foo" at the repl.
After running the "intros" tactic, it gave you:
---------- Assumptions: ----------
k : Nat
inductiveHypothesis : plus k 0 = k
---------- Goal: ----------
{hole_2} : S (plus k 0) = S k
At which point you would apply the "rewrite" tactic with your inductive hypothesis. Yes, I was wondering why that was, I assumed it was giving 'rewrite' (or the human reader) some clue about what the property was. |
==> and <== were introduced in a blog post by Edwin Brady which I can't find at the moment - maybe we could find where that went later. From what I recall, and looking at that, I thought it was a way of supplying a goal type or target to your rewrite, to better tell Idris how to apply the rewrite and to get better error messages if it didn't work, and as documentation for yourself. |
but I would like to try to understand rewrite without the syntactic sugar so that I can go on to more complicated examples with some intuition.
Some nores from this thread:
Generally proof equations are written as complexity-reducing devices, with the more complex part on the left and the less complex on the right. For example, the monoid neutral law looks like n + 0 = n, because n is simpler than n + 0. But with factors, the reduction in complexity is to say that a larger number can be written as the product of smaller numbers, so I think n = p * q is appropriate. I try to use rewrite rather than replace whenever I can, but it's not always possible. There is the huge difference between them, however. replace makes a substitution in a proof you already have to create another proof. rewrite makes a substitution in the goal (which is a proof you do not have yet) instead. In practice it means that with rewrite you work kind of backwards, rewriting your goal until it matches something you already have, while replace has a more direct approach. Also with rewrite you can only use equality (=) proofs (the same with replace of course), which means that you you need use a custom proof-altering function like cong or something in the middle of replacements, you actually can no longer use rewrite from that point on. |
For some reason I don't feel I am going to understand 'rewrite' fully unless I can do it using 'replace'.
This is my attempt but it fails (Unifying n and S n would lead to infinite value):
prop : (x : Nat) -> Type
prop x = (plus x Z) = x
total plusZeroRightNeutralRep : (x : Nat) -> (plus x Z) = x
plusZeroRightNeutralRep Z = Refl
plusZeroRightNeutralRep (S n) =
let m = (S n) in
replace {P = prop} (the (m = (S n)) Refl) plusZeroRightNeutralRep n
Replace
Parity may have some interesting examples.
This implements the indiscernability of identicals principle, if two terms are equal then they have the same properties. In other words, if ``x=y``, then we can substitute ``y`` for ``x`` in any expression. In our proofs we can express this as:
if x=y
then P x = P y |
where ``P`` is a pure function representing the property. In the examples below ``P`` is an expression in some variable with a type like this: ``P: n -> Type``.
So if ``n`` is a natural number variable then ``P`` could be something like ``2*n + 3``.
To use this in our proofs there is the following function in the prelude:
||| Perform substitution in a term according to some equality.
replace : {a:_} -> {x:_} -> {y:_} -> {P : a -> Type} -> x = y -> P x -> P y
replace Refl prf = prf |
Removing the implicits, if we supply an equality ``x=y`` and a proof of a property of ``x`` (i.e. ``P x``) then we get a proof of a property of ``y`` (i.e. ``P y``)
> :t replace
replace : (x = y) -> P x -> P y |
| So we can call replace like this: |
|
This replaces (x=plus x Z) with (y=plus y Z). To do this replace infers the property: P x is (x=plus x Z).
This example does not really do anything, it just changes the name of the variable (α-conversion in lambda calculus).
| A more useful example would be something like this: |
|
| but this produces this error: |
|
| It doesn't seem to be able to infer P in this case so we need to help it by suppling the property like this: |
|
So can we prove (x=plus x Z) for all values of x?
Since we can't have an infinite number of cases like this: we need to do it recursivly. |
|
Or change it so left and right depend on the same natural number. |
|
We need a case that says that if 'plusZeroRightNeutral3 x' constructs Refl then 'plusZeroRightNeutral3 (S x)' will constructs Refl.
If we replace the literal natural numbers with 'n' like this: |
|
then we get this error |
|
Another Example
Example from: Idris-dev/samples/tutorial/Theorems.idr and test/tutorial004/tutorial004.idr |
|
This takes the equation 'Z = S n'
and subsitites to 'Void = ()' which does not have a constructor so is Void.
Rewrite
https://medium.com/@prozacchiwawa/beginner-notes-on-proofs-in-idris-f7322cbe2086
| rewrite t in Refl | takes Refl : left = right object and expr : t. Searches left in t. Replaces all occurrences of left with right in t |
Like replace, rewrite can apply substitutions but is built into the Idris syntax and not purely a library function. In addition to the special syntax there are differences from replace.
| Here is the rewrite syntax (from Idris-dev/src/Idris/Parser/Expr.hs): |
|
there is an optional '==>' term
| So when the compiler encounters 'rewrite' it infers the property 'P' and then uses rewrite__impl from libs/prelude/Builtins.idr |
|
Rewrite can be dificult to use and debug. This is because the intemediate values of types are not always given in the source code and since we are relying on the automatic pattern matching and normalisation that the compiler does. So there may not be many clues to the reader of the source code. When debuging we tend to get error messages like:
- rewrite did not change the type
- Unifying n and S n would lead to infinite value
Which don't give many clues about what is going on.
There is ==> and <==, to add extra type annotations to rewrite: http://docs.idris-lang.org/en/latest/reference/misc.html#match-application but these are not fully documented and are seldom used.
| Here is an example: | rewrite ((m + Z = m) <== plusZeroRightNeutral) ==>
(Z + m = m) in Refl |
This is linked as a syntax example from release notes (http://www.idris-lang.org/idris-0-9-9-released/), but has bitrotted. A up-to-date example version of this can be found in the tests: https://github.com/idris-lang/Idris-dev/blob/master/test/proof001/test029.idr |
plus_comm : (n : Nat) -> (m : Nat) -> (n + m = m + n)
-- Base case
(O + m = m + O) <== plus_comm =
rewrite ((m + O = m)
<== plusZeroRightNeutral) ==>
(O + m = m) in refl
-- Step case
(S k + m = m + S k) <== plus_comm =
rewrite ((k + m = m + k)
<== plus_comm) in
rewrite ((S (m + k) = m + S k)
<== plusSuccRightSucc) in
refl |
If both sides of the equation don't normalise to the same value/type then we may be able to use rewrite so they do:
plus_commutes_Z : m = plus m 0
plus_commutes_Z {m = Z} = Refl
plus_commutes_Z {m = (S k)} = let rec = plus_commutes_Z {m=k} in
rewrite rec in Refl |
For instance, in this example:
What is the type of this last Refl?
I would be expecting something like m=(S n) so it would rewrite
(plus (S n) 0 = (S n)) as (plus m 0 = m) but how do you introduce a new variable and prove that it is equal to something?
If I put a hole like this: rewrite inductiveHypothesis in ?myrefl I get: Holes: Main.myrefl
|
So how does that work? 'm' and 'plus m 0' dont normalise to the same value so how can Refl construct the type 'm = plus m 0' ?
| If we have | X:x=z | |
| then | rewrite X in Y |
will do a substitution to replace all occurences of x with y in Y.
replace : (x = y) -> P x -> P y |
Given a proof that x = y, and a property P which holds for x, we can get a proof of the same property for y, because we know x and y must be the same. In practice, this function can be a little tricky to use because in general the implicit argument P can be hard to infer by unification, so Idris provides a high level syntax which calculates the property and applies replace:
I am trying to find a simple example to experiment with rewrite:
| It does not seem to make sence using rewrite with literal values: | testRewriteNull: Z=Z testRewriteNull = rewrite (the (Z=Z) Refl) in Refl |
| because any rewrite is trivial: | |
135 | testRewriteNull = rewrite (the (Z=Z) Refl) in Refl
| ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
When checking right hand side of testRewriteNull with
expected type
0 = 0
rewriting 0 to 0 did not change type 0 = 0
|
| So, to demonstrate rewrite, we need to find an example with variables: | testRewriteNull: (a:Nat) -> a=a testRewriteNull a = rewrite (the (a=a) Refl) in Refl |
| even so we still need more structure for a meaningful example: | |
135 | testRewriteNull a = rewrite (the (a=a) Refl) in Refl
| ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
When checking right hand side of testRewriteNull with
expected type
a = a
rewriting a to a did not change type a = a |
| Proving x = x + Z is the simplest meaningfull example I can think of: |  |
rewrite prf in expr If we have prf : x = y, and the required type for expr is some property of x, the rewrite ... in syntax will search for x in the required type of expr and replace it with y for example rewrite x=y in x=x+0 gives y=y+0 so rewrite (S n)=n in 5=5+0 gives 4=4+0 |
total plusZeroRightNeutral2 : (x : Nat) -> (plus x Z) = x
plusZeroRightNeutral2 Z = Refl
plusZeroRightNeutral2 (S n) =
let inductiveHypothesis = plusZeroRightNeutral2 n in
rewrite inductiveHypothesis in Refl
|
-- without 'let'
total plusZeroRightNeutral21 : (x : Nat) -> (plus x Z) = x
plusZeroRightNeutral21 Z = Refl
plusZeroRightNeutral21 (S n) =
rewrite (plusZeroRightNeutral21 n) in Refl |
|
prop : (x : Nat) -> Type prop x = (plus x Z) = x propS : (x : Nat) -> Type propS x = (plus (S x) Z) = (S x) propRev : (x : Nat) -> Type propRev x = x = (plus x Z) |
|
rewrite__impl requires an explicit property This gives an error: |
plusZeroRightNeutral21x : (x : Nat) -> (plus x Z) = x
plusZeroRightNeutral21x Z = Refl
plusZeroRightNeutral21x (S n) =
rewrite__impl prop (plusZeroRightNeutral21x n) Refl
When checking right hand side of
plusZeroRightNeutral21x with expected type
plus (S n) 0 = S n
When checking an application of function rewrite__impl:
Type mismatch between
n = n (Type of Refl)
and
prop n (Expected type)
Specifically:
Type mismatch between
n
and
plus n 0
Holes: Main.plusZeroRightNeutral21x
|
try changing (plus x Z) = x to x = (plus x Z) which now gives this error:
|
plusZeroRightNeutral21xr : (x : Nat) -> x = (plus x Z)
plusZeroRightNeutral21xr Z = Refl
plusZeroRightNeutral21xr (S n) =
let inductiveHypothesis = plusZeroRightNeutral21xr n in
rewrite__impl propRev inductiveHypothesis Refl
|
127 | rewrite__impl propRev inductiveHypothesis Refl
| ~~~~~~~~~~~~~~~~~~~
When checking right hand side of
plusZeroRightNeutral21xr with expected type
S n = plus (S n) 0
When checking an application of function rewrite__impl:
Unifying n and S n would lead to infinite value
Holes: Main.plusZeroRightNeutral21xr
|
Try defining simpler examples:
| x |
-- rewrite__impl requires an explicit property
testRewritex3: (y=x) -> (prop x) -> (prop y)
testRewritex3 a b = rewrite__impl prop a b
testRewritex: {x,y:Nat} -> (y=x) -> (prop x) -> (prop y)
testRewritex a b = rewrite a in b |
see this thread
One of the difficulties of writing programs with dependent types is that when you write a function
implementation, you have to prove that the type of the returned value is the same as that in the
definition.
Replace and rewrite do that but the syntax used in them can hinder the readability of the code,
making very simple proofs very difficult for no reason.
There is a nice syntax for rewrite that is like this:
rewrite ((m + Z = m) <== plusZeroRightNeutral) ==>
(Z + m = m) in Refl
as can be seen in misc.rst
but it is not adequately documented.
This syntax is nice because when someone reviews the proof, they can see the changed type
as is common in mathematical proofs.
A secondary issue regarding the readability of the code when using rewrite and the "match"
application syntax can be found in #3425. |
The difference from ``replace`` above is nicer syntax and the property ``p1`` is explicitly supplied and it goes in the opposite direction (input and output reversed).
Example: again we supply ``p1`` which is a proof that ``x=2`` and the equality ``x=y`` then we get a proof that ``y=2``.
p1: Nat -> Type
p1 x = (x=2)
testRewrite2: (x=y) -> (p1 y) -> (p1 x)
testRewrite2 a b = rewrite a in b |
We can think of rewrite doing this:
- start with a equation ``x=y`` and a property ``P: x -> Type``;
- search ``y`` in ``P``;
- replace all occurrences of ``y`` with ``x`` in ``P``.
That is, we are doing a substitution.
testRewrite: (x=y) -> (p1 y) -> (p1 x) testRewrite a b = rewrite__impl p1 a b |
Issues
From Wikipedia: In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with functions of other variables. The intent is that when expressed in new variables, the problem may become simpler, or equivalent to a better understood problem. |
In Idris we need to be able to prove that equations represent the same type, for instance, if a function requires a term of the type: 'x=x+0' can we pass it a term of the type: 'x=x+0' or pehaps '2=2+0'?
Note on terminology: strictly there is a distiction between the term 'substitution' and 'change of variables'. In a system of equations we can only change variable if it is not used in the other equations. For instance: The equation 'x=x+0' expresses the same identity as 'y=y+0'. The name of the variable does not matter (a bit like alpha equivalence in lambda calculus where the choice of a bound variable name does not matter provided it is not bound to an outer term). |