This is one of a set of pages about the Axiom CAS and its forks, particularly FriCAS, these pages start here. This particular page discusses the language used by FriCAS which is called SPAD. This page is a general overview of SPAD but, for an attempt at a more rigorous definition, see the syntax page.
Spad is a language for the Axiom/FriCAS symbolic computing mathematics program. The language can be used interactively as an interpreter, here we discuss its use to define new packages and domains by compiling from an '.spad' file. So just to be clear this page concerns the Spad compiler and not the Spad interpreter (these sometimes produce different results).
There are some specific requirements for a language to support a CAS. If we were to start to write some code to support some given algebra (say - vectors) then we soon find we need to use dependant types (or at least some weaker form of dependant types), we then need to make some tradeoffs between this requirement and type safety and things get messy. As far as I know, no mainstream, statically typed languages support dependant types, perhaps some variants of ML?
Therefore we need to investigate CAS programs that are designed specifically to support user defined algebras.
On this page the Spad language is compared with the Object Oriented (OO) and Functional Programming methodologies. If you are new to programming it is better to stick to the proper documentation:
However, Spad looks very similar to other languages, but there are subtle differences which can cause confusion to the unwary. So, for my own use,I find it useful to keep this record of the differences and also a crib sheet for the SPAD syntax. I have left it here in case it is useful for others. In addition to this, as an exercise to see what is special about SPAD and what makes SPAD different from general purpose computer languages, I have been investigating whether SPAD functionality could be implemented in other languages such as Scala (see my initial thoughts about this on this page).
Computer Algebra using OO and Functional Methodologies
So what are the special requirements of a maths program? How does it affect the best computer language and methodology to use? Lets take an example of representing a simple equation such as:
force = mass * acceleration
We could represent this using OO methodology, for example the variables force and acceleration could be instances of a vector class, mass could be an instance of a real class and '=','*' can then represent functions on these objects. However this does not work very well in practice because:
- The operations like '*' cut across different objects. (We could get round this by putting scalar*vector in class vector and scalar*scalar in class real but this gets more complicated when we add more classes and functions).
- If we already know that mass is of type real and acceleration is of type vector then we can infer the type of force, or we may want to infer the type of mass or acceleration. But we cant use objects until we know what type they are, we need a more dynamic matching approach.
- We need a way to support 2D or 3D vectors and so on, also vectors over reals or vectors over integers and so on.
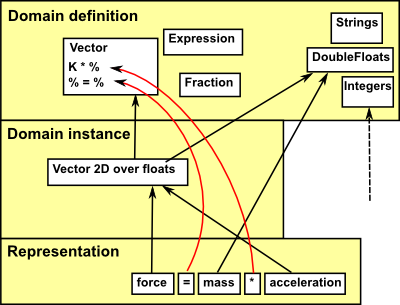
So, unless we are only using built-in ('static') types like Integer, DoubleReal, List and String then there are two levels of instantiation, first we instantiate the type(s), then we instantiate the representation:
(1) -> force := vector([0$DoubleFloat,1])*9.81
(1) [0.0,9.809999999999999]
Type: Vector(DoubleFloat)
|
So a type Vector is created by: vector([0$DoubleFloat,1]) but I don't really understand what is going here? If a 2 dimensional vector over DoubleFloat is created several times:
(2) -> cosAngle := dot(vector([0$DoubleFloat,1]),_
vector([0$DoubleFloat,2]))/2
(2) 1.0
Type: DoubleFloat
|
Is there a separate type for each of these?
The following quote is taken from the FriCAS forum here
> I think part of my problem is that I am not clear about domains like
> Float and OutputForm that are not explicitly created by the user, are
> instances created when needed by the system, or does the same one
> remain active through the session?
When you write '1::OutputForm', you in particular request sytem to
create (possibly new) instance of OutputForm. Basically any code
that uses some domain is in some sense requesting creating this domain.
However, actual creation is done in lazy way (and split into several
steps), and AFAIK typicall domains are actually in a strange "almost
done" state. Domain creation is rather expensive, so once FriCAS
stared creating a domain (that is created a stub ready to fill
details in lazy way) it will normally reuse the already created
part. Some domains are marked as "mutable", FriCAS will not
re-use such domains but create new instance.
Above I wrote "normally" because cache (such caches are per
constructor) holding already created domains may overflow and
then FriCAS will remove the oldest position for the cache.
And user may explicitly clear caches using ')clear completely'.
Also Spad complation clears caches.
Because OutputForm has no parameters, it needs cache with single
slot and this cache will never overflow, so normally you will
re-use old version. But if caches are cleared, new instance
is created.
BTW: Normally persistent state is stored in Lisp variables, you
can access them from Spad (but they must be created from Boot or
Lisp). Float is not really good example, basically I think it
is better to avoid variables in domains (but Float has specific
needs so it is not clear if we can do better).
--
Waldek Hebisch |
Functions
Most of the 'processing' done by an SPAD program is done by functions, for example here we define a function called 'force' and then use it to calculate the force required to accelerate a mass of 2 units by an acceleration of 3 units.
(1) -> DF ==> DoubleFloat
Type: Void
(2) -> force(m:DF,a:DF):DF == m*a
Function declaration force : (DoubleFloat,DoubleFloat) ->
DoubleFloat has been added to workspace.
Type: Void
(3) -> force(2,3)
Compiling function force with type (DoubleFloat,DoubleFloat) ->
DoubleFloat
(3) 6.0
Type: DoubleFloat |
When defining a function in the compiler then we may specify the function in two stages:
- function declaration - force: (DF,DF) -> DF this defines the 'signature' of the function this allows the program
- function definition - force(m,a) == m*a
So if a function like force(2,3) is called the program will recognize this as a function call and search the functions that have been stored in the program for a match. Both the function name and the number and type of input and output parameters must match, this comes from the signature from the declaration. When
Functions can have multiple input parameters but only one output (i.e. return) parameter
SPAD does not make a distinction between 'pure' functions and functions with 'side-effects' such as outputting or inputting, or writing to a global variable, or modifying an input parameter. However there are some conventions such as adding a ! to the name of a function which modifies its input parameters.
Each parameter has a type, types may be:
- Built in types.
- User defined types, such as a user defined domain as described later.
- Functions (the type of a function is its signature like: (DF,DF) -> DF).
Packages
Function declarations and definitions may be grouped together into a package. Often this is just a convenient way to keep related function declarations/definitions together but it can provide additional control over which function gets called in cases where several signatures would match.
This is done by specifying the package using the '$' symbol.
myFunction(2,3)$myPackage
So a package is starting to look a bit like an 'object' but only in that it is grouping functions together its not doing things like data abstraction, encapsulation, polymorphism and so on.
More about packages below.
Domains
A domain is like a package but with an additional capability, it allows us to create a variable called Rep which allows us to create runtime instances.
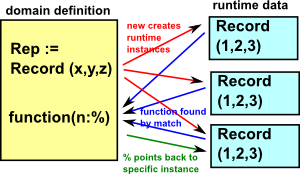
More about domains below.
Object Oriented - Similarities and Differences
In object oriented (OO) programs the data and the functions on that data are linked by putting them in a class definition. This provides data abstraction and encapsulation, because classes can hide the details of their implementation from their clients.
So for an object oriented program:
| class definition: |
| variables, every time this class is instantiated, by 'new' keyword, storage for these variables is allocated and they are set to their initial values with some internal link back to these function definitions. |
| functions which can be applied to the particular instance of the object. |
|
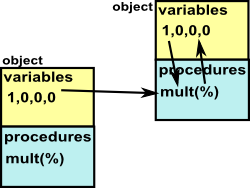
Spad can operate in this way, for instance mult could be defined as unary function which could be called like:
| java |
Spad |
| a.mult(b) |
mult(b)$a |
to mean a*b. There is a problem with this, if we did this we would have to create a different type for a and b. Although we can do this with Spad packages, domains give a better solution by using 'representations': |
 |
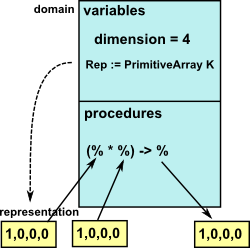
| In Spad Domains we can create one instance of a type, for instance CliffordAlgebra, then multiplication is a binary function which takes two arrays representing the multivector and returning the result as a similar array. Note that these arrays are not held in the domain but their type is held in the Rep variable. |
 |
This is much more of a mathematical approach because:
- Multiplication is a binary function (%, %) -> % where % is a placeholder for the underlying set.
- '*' is defined for different types and we want to choose the type to operate on by matching (rather than specifying the type with $a).
- This approach is closer to the functional programming approach (see below) which has the potential for additional benefits.
So how does spad match an instance of a domain to the function definition? It associates the function with the 'class' (domain) by pattern matching.
However, the program still needs to know how to associate these arrays to their function definitions, I assume that when an instance is created using the 'new' statement adds a link back to the function definition. When the CliffordAlgebra multiplication function returns a new array representing the result it creates it like this:
Impl ==> add
dim := 2^n
Rep := PrimitiveArray K
New ==> new(dim, 0$K)$Rep
In most OO languages there is a 'this' keyword, so that the code in functions can refer to the object that contains it, I get the impression that in Spad this is divided into two parts.
| % |
this type (domain)
typically used for matching a function such as:
(%, %) -> % |
| Rep |
this representation |
I would like to understand this better, for instance,
- Can I use any structure for the representation, such as List [], Tuple () or String "" ?
- What is PrimitiveArray? I can't find this in the documentation.
- How does the domain use the Rep parameter? Rep does not even hold the size of the PrimitiveArray.
- How should an instance of potentially sparse instance be created?
The following quote is taken from the FriCAS forum here (see references at the end of this page)
You ask "So how does spad match an instance of a domain to the function definition?". This is not well-posed question. You probably want to know how Spad decides which function to call. This is two stage process. The first stage is overload resolution at compile time. In given call place there may be several (or none) visible definitions for given function. Each definition comes from some domain or package. Recall that domains and package are computed at runtime: the Spad compiler knows how to compute appropriate domains and for each of them knows associated category. Note that category is known at compile time and gives list of functions available in the domain (the domain may export more functions, but the compiler only uses compile-time information about available functions). Given list of available functions Spad compile tries each in turn to see if types of arguments agree with function declaration and if the result type is acceptable. Note that Spad allows you to have multiple functions with the same argument types, which differ only in the result type, so the expected result type affects choice and complicates the resolution process. Let me say that it may be hard for programmer to predict which function will be used by the compiler, if that is a problem the programmer may explicitly specify types, like:
(foo(x1@Type1, x2@Type2)$Type3)@Type4
which means that the compiler will check that x1 is of type Type1, x2 is of type Type2 and then search domain (or package) Type4 for function foo which takes arguments of types Type1 and Type2 and returns value of type Type3. Let me add that code for resolving overloading in the compiler is not very large, but in a sense it is most complicated part of Spad compiler. Actually, the problem with overloading is that it is impossible to do "right thing" with reasonable efficiency, so the compiler takes shortcuts which make hard to describe what the compiler is actually doing.
Now, you may think that overload resolution chooses concrete function to call, but in fact there is more to this. First, list of available functions is known at compile-time, but the domain may be only known at runtime -- this is quite similar to Java where interface in statically known, but actually object class in known only at runtime. Second, the function in not necessarily implemented in given domain -- it may be inherited. This requires runtime search. While inheritance have similarity to typical OO languages, there are significant differences. |
Definition and Implementation
In some OO languages such as as C++ a function can be separately declared (in .h file) and defined (in .cpp file). In other languages such as java there is no separate declaration.
In Spad if a function is required outside the domain (it is exported) then it requires both a definition and an implementation. If it is local then only an implementation is required but it will only be seen after the implementation, that is, we only use a local function below the place in the file where it is defined.
*: (%, %) -> %
in the category part (which is the "interface", i.e. the names of exported functions) and
(a: %) * (b: %): % == ...
in the implementations part (the stuff that comes after the "add" keyword). |
Inheritance and Composition
In OO languages we can inherit from a superclass, in a hierarchy, and our object will behave as if it were an object of the superclass. Our class can provide additional functions and can also 'overload' a function, that is use the same signature as a function in the superclass, thereby customising the functionality.
Spad supports (multiple) inheritance, Polymorphism only works when we inherit from categories (see polymorphism example below). Categories (not to be confused with category theory?) are a bit like java interfaces but they allow implementations as well as definitions of functions.
Multiple inheritance from categories can be done like this:
T ==> Join(Ring, Algebra(K)) with
and categories can inherit from other categories in a hierarchical structure.
How are conflicts handled in multiple inheritance?
How do we design the category hierarchy? I have thought about some of the issues for the case of Clifford algebra on this page.
Polymorphism
Many classes can implement the same interface, this allows us to access different types of data as if it were the same (through the same interface).
In java the inheritance and polymorphism concepts are separated In C++ polymorphism can be done by multiple inheritance and vitalization, in java there is an interface which is separate from inheritance.
The following quote is taken from the FriCAS forum here (see references at the end of this page)
> Concerning OO, Spad gives you some OO capabilities, but they are
> different than in other languages. You may use Spad categories
> like Java interfaces and domains like classes, but while
> inheritance for categories works like in Java, inheritance for
> domains is different (in C++ speak all methods defined in a
> domain are static).
Oh, that is true and will probably bite you some day. If you have a domain (modify Integer)
and you say
a: A := 7
b: B := 7
g(a)$A
g(b)$B
They will give the same result, since functions are not "virtual" in SPAD. B inherits the full implementation of g from A. So when you call g(b)$B you actually call g(b)$A. Since that does not type check (the argument of g$A must be of type A but b is of type B, it rather calls
g(b pretend A)$A
Anyway, the implementation of f$B does not matter for the evaluation of g(b). To see a full work through of this example see 'virtual function example' on this page. |
 |
|
Functional Programming - Similarities and Differences
The ideas of functional languages go back to lambda calculus (Is there a domain for lambda calculus?)
Functional programs tend to have the following properties:
- functions are first class objects, they can be passed to and returned from other functions, they can be stored in variables and so on.
- discourages 'side effects' of functions such as modifying variables that can be seen outside the function. That is functions tend to purely map inputs to outputs like mathematical functions.
- Functional style:
- The constructs in the language tend to be functions.
- encourages immutable objects (although lists are mutable)
- encourages recursion over iteration.
- If we took this to extremes values might be defined in terms of functions, functions of functions and so on back to fundamental values such as 0 and 1.
In Spad functions may return types, as well as functions or values.
The following quote is taken from the FriCAS forum here (see references at the end of this page)
No, values are not "defined in terms of functions".
Rather: the only way to get a value is by applying a function of the appropriate domain.
There is an exception (in spad, not aldor): for "literals", i.e., Integers, DoubleFloats, Strings there are no functions.
"everything is a function" -- this is confused. Spad has functional interfaces, meaning that you can not directly get domain data (in Java speak all member variables are private and you can get them only if there is appropriate accessor function). Spad uses functional notation of other operations:
a(b)
may be:
- function a applied to b
- element number b of array a
- element number b on list a
- field b of record a
- something different if appropriate 'apply' operation is defined
but application is not always defined, for example '1(2)' does not "work". |
Program Structure Elements
Blocks are indicated by indentation (either spaces or tabs - any preferred recommendation? two spaces per indent?) not by curly bases.
Statements can be separated by ';' but this only tends to be used when statements are on the same line or to avoid ambiguous statements.
Types are also only needed to avoid ambiguity, for instance,
a : Integer := 2
or
a := 2$Integer
The brackets () around a function call are optional when the function takes only one argument. This makes a function equivalent to an infix operator.
symbol
(keyword) |
description |
example |
| f : (arguments) -> returnType |
function declaration |
t : (Float -> Float, Float) -> Float |
| == |
rule, delayed assignment
function definition |
fact(0) == 1
fact(n) == n*fact(n-1)
t(fun, x) == fun(x)**2 + sin(x)**2 |
| var +-> function |
+-> is an infix operator meaning 'maps-to'
It can be used to create anonymous functions, so instead of:
myFunct(x:Type):Type == if x >0 then x else -x
we can have:
x +-> if x >0 then x else -x |
x +-> if x >0 then x else -x |
| name macro == body |
macro is a general textual substitution |
|
==>
macro name == body
macro name(arg1,...) == body |
macro definition
provides general textual substitution |
NNI==> NonNegativeInteger
T ==> Join(Ring, Algebra(K), VectorSpace(K)) with |
| g(arg1: INT, arg2: FLOAT, arg3: INT): STRING == ... |
function combined declaration and definition |
|
| := |
immediate assignment
multiple immediate assignment |
variable := expression
( var1, var2, ...,
varN ) := ( expr1, expr2,
..., exprN ) |
| :* |
|
|
| = |
equation |
|
| PackageForm : Exports == Implementation |
simplified package definition |
|
PackageForm : Exports == Implementation where
optional type declarations
Exports == with
list of exported operations
Implementation == add
list of function definitions for exported operations |
package definition |
|
| DomainForm : Exports == Implementation |
simplified domain definition |
|
DomainForm : Exports == Implementation where
optional type declarations
Exports == [ Category Assertions] with
list of exported operations
Implementation == [ Add Domain] add
[Rep := Representation]
list of function definitions for exported operations |
domain definition |
|
| CategoryForm : Category == Extensions [ with Exports ] |
category |
|
| import domain |
capsule |
add
inport RepeatedSquaring($) |
| statement ; |
mark end of statement, not usually required unless we put more than one statement on a line. |
a:=1;b:=2 |
| : Type |
indicates type |
a : Integer := 2 |
| :: Type |
convert to type |
|
| pretend Type |
treat one type as another, only works if they have the same internal structure (how do I know what the internal structure is?) |
(2/3) pretend Complex Integer |
$
function() $Type
variable $ Type |
specify domain
call function for a given type
force variable to a given type |
new(dim, 0$K)$Rep
sin(4.3) $Float
4.3$Float |
| calculation @ Type |
tell Axiom the desired type of a result of a calculation |
(1) -> (1 + 2)@Float
(1) 3.0
Type: Float |
| free variable |
allows us to declare a variable that is global |
free counter |
| local variable |
allows us to declare a variable that is not global |
local counter |
| ( ) |
tuple (array of different types)
parameters for a function are a tuple, so prefix operator on a tuple is equivalent to a function. |
(1) -> (1,2,3)
(1) [1,2,3]
Type: Tuple(PositiveInteger)
|
| [ ] |
list literal (mutable array of items with the same type)
many functions availible see List below
Also used for Records and Unions (like lists but elements may be of different types and elements have selector) |
(1) -> [1,1,2]
(1) [1,1,2]
Type: List(PositiveInteger)
[2^i for i in l] |
| { } |
In FriCAS now block delimiter
Was
Set ( like list but order unimportant ) |
(1) -> set [1,1,2,3,3]
(1) {1,2,3}
Type: Set(PositiveInteger)
|
| " " |
string literal (array of char) |
|
if boolean then
if equation then
if ... not ... and ...or ... then
if ... then ... else ...
|
if ... then [else ...] always returns a value so we can use this on the right hand side of an assignment
since there is an explicit 'then' keyword there is no need to put the condition in brackets |
a:= if x >0 then x else -x |
| if R has Field then ... |
|
|
| if myUnion case mtType then ... |
Select from Union values |
if not (n.parameters case boundbox) then |
| BoolExpr=>Expr |
if BoolExpr is true then return from block with value Expr |
~prime?(i) => iterate |
| ~= |
returns true if both sides not equal |
|
| _ |
escape character and continue on next line if at the end of a line |
_" to put " into a string |
| -- |
comment for rest of line |
|
| ++ |
comment for following variable, function, etc. |
|
| % |
this domain |
|
| while BoolExpr repeat loopBody |
|
|
| do |
|
|
while
...repeat ... iterate ... |
skips over the remainder of a loop |
if odd? then () iterate |
| break |
leave current loop |
|
| return |
leave current function |
|
for i in n..m repeat ... is 1
for i in n..m by s repeat ...
for i in list repeat ...
for j in n..m repeat loopBody
for j in n..m | odd? j repeat
|
|
for i in n..m repeat ... is 1
for i in list repeat ...
for j in 200..300 repeat loopBody
for j in 200..300 repeat loopBody
for j in 200..300 by s repeat... |
| default |
|
|
| define |
|
|
| export |
|
|
| extend |
|
|
| fluid |
fluid variables are bound to a function and can be used by functions it calls. |
|
| from |
|
|
| generate |
|
|
| goto |
fortran code |
|
| inline |
|
|
| never |
|
|
| of |
|
|
| to |
|
|
| yield |
|
|
| . |
|
|
| , |
|
|
| ' |
|
|
Common Types
Definable Operators
| by |
case |
mod |
quo |
rem |
|
| |
|
|
|
|
|
| # |
+ |
- |
+- |
~ |
^ |
| * |
** |
.. |
= |
~= |
^= |
| / |
\ |
/\ |
\/ |
< |
> |
| <= |
>= |
<< |
>> |
<- |
-> |
I have listed some of the built-in types and the functions defined on them here:
| |
Boolean |
Z
Integer |
PI
PositiveInteger |
Equation |
Symbolic |
| + |
|
|
?+? |
|
|
| - |
|
|
|
|
|
| * |
|
|
?*? |
|
|
| / |
|
|
recip |
|
|
| power |
|
|
?^? |
|
|
| and |
?/\?
?and? |
|
|
|
|
| or |
?\/?
?or? |
|
|
|
|
| ~ |
not |
|
|
|
|
| nand |
nand(%,%) |
|
|
|
|
| nor |
nor(%,%) |
|
|
|
|
| xor |
xor(%,%) |
|
|
|
|
| = |
?=? |
|
?=? |
|
|
| ~= |
?~=? |
|
?~=? |
|
|
| > |
?>? |
|
?>? |
|
|
| < |
?<? |
|
?<?
smaller?(%,%) |
|
|
| >= |
?>=? |
|
?>=? |
|
|
| <= |
?<=? |
|
?<=? |
|
|
| max |
max(%,%) |
|
max : (%,%) |
|
|
| min |
min(%,%) |
|
min : (%,%) |
|
|
| not |
not? |
|
|
|
|
| random |
|
|
|
|
|
| gcd |
|
|
gcd(%,%) |
|
|
| |
|
|
|
|
|
| constants |
false
true |
|
1 |
|
|
| test |
|
|
one? : % |
|
|
| odd? |
|
|
|
|
|
| bit? |
|
|
|
|
|
to see exports for a given type:
)show Boolean
Common Functions
I have listed some of the functions that are common to a lot of domains here:
| Function |
Use |
| reduce |
the reduce operation is used to extend binary operations to more than two arguments
reduce(binary function,List of operands, initial value)
reduce(max,[2,3,7,3,-4])
(((A,B) -> B),List A,B) -> B
successively uses the binary function (A,B) -> B on the elements of the list and the results of previous applications |
| |
|
Lisp Functions
Lisp is the underlying runtime environment and SPAD relies on direct calls to Lisp to provide basic functionality. The names of these function calls end with $Lisp.
I have started making a list of these function calls on the page here.
Input / Output
SPAD domains can define how a given algebra will be displayed on the output device. How that works is explained on the page here.
Lists
I get the impression that
elt(list,index)
list . index |
extract the first element at index |
|
| .. |
segment |
1..10 |
| for var in seg repeat loopBody |
loop through segment |
m := matrix [ [4*i + j for j in 1..4] for i in 0..3] |
| for var in list repeat loopBody |
loop through list |
|
| for var in seg | BoolExpr repeat loopBody |
such that (must be boolean) |
|
| # |
size of |
|
| |
|
|
Statically Typed
Is statically typed, i.e. types of elements are known at compile time.
Package
Package is similar to a class definition in OO and it is also a function which returns an implementation. However it is not really like a OO class because, although the following package constructor looks like an OO constructor the parameters UP and Par are part of the package type (like generics) they are not intended as parameters set differently each time an individual instance is created and they can't be modified by functions.
ComplexRootPackage(UP,Par) : T == C where
UP : UnivariatePolynomialCategory Complex Integer
Par : Join(Field, OrderedRing)
T == with |
So a package is really intended as a collection of function calls which are self contained but perhaps share generic types. In other words a package does not have a set of changeable parameters that could be set and read by functions. The general form is:
PackageForm : Exports == Implementation
Since, in practice we need declarations and implementations, it is usually used in an extended form:
PackageForm : Exports == Implementation where
optional type declarations
Exports == with
list of exported operations
Implementation == add
list of function definitions for exported operations |
There are two parts to this:
- The first part contains the function declarations (named Exports here but could be called anything), this declares the 'signature' of the function which is exported (made available to the rest of the code and to the interpreter). This is a bit like an interface definition to the rest of the system.
- The second part contains the function definitions (named Implementation here but could be called anything), this defines the body of the functions, is defines what the function actually does.
All operations have types expressed as mappings with the syntax:
source -> target
Domain
This is similar to package with the addition of a representation, it is also a function which returns an implementation:
DomainForm : Exports == Implementation
Again this is usually extended to:
DomainForm : Exports == Implementation where
optional type declarations
Exports == [ Category Assertions] with
list of exported operations
Implementation == [ Add Domain] add
[Rep := Representation]
list of function definitions for exported operations |
Representation Example:
Rep := SquareMatrix(n,K) --representation
One of the differences from package is the special variable Rep to identify the lower level data type used to represent the objects representation of the domain.
representation
The Rep for quadratic forms is SquareMatrix(n, K).
This means that all objects of the domain are required to be n by n matrices with elements from K.
Category
CategoryForm : Category == Extensions [ with Exports ]
Each exported operation has a name and a type expressed by a
declaration of the form
``name: type''.
Categories can export symbols, as well as
0 and 1 which denote
domain constants.The
numbers 0 and 1 are operation names in Axiom.
In the current implementation, all other exports are operations with
types expressed as mappings with the syntax
source -> target
Performance Issues
When writing a program it is useful to have some sore of model in ones head of how to write efficient code. Otherwise there is no way to guess which is best without actually timing the output.
- What are performance issues of recursion verses iteration? Is tail recursion better and so on?
- Does Spad use garbage collection?
To help with these
The following quote is taken from the FriCAS forum here (see references at the end of this page)
Spad distinctive feature is its type system. Spad is "statically typed" meaning that compiler knows how to compute "static" type for each quantity. I put "static" in quotes because in Spad types are actually computed at runtime (in some cases Spad compiler can determine type already during compilation, but frequently it can not). Spad is different from dynamically typed languanges which bundle type information with actual data -- in Spad type information is separate. This means that Spad compiler has a lot of opportunities to omit computations on types. Spad approach is also different than typical OO approcach: in Java interfce is statically known but at runtime you may have any object which satisfies given interface. So in practice Jave also have to bundle object type (class) with data. In Spad OO type inheritance is is available ony for categories (types of types), but not for normal data. So for normal data type computed by the compiler exactly agrees with actual type of data.
I should mention here that many of Spad types are parametrised, for each tuple of parameteres you get distinct type. Spad types may be passed as arguments to functions and returned as values -- this in principle gives quite a lot of possibilites to do computations on types. Let me add that types computed at runtime pose a significant challenge for the compiler, especially that Spad has type-based overloading -- there is a risk that compiler will be forced the generate very inefficient code. Spad solves most of this problem putting some extra restricions: you are not allowed to do general runtime computation on categories, all categories (except for exact values of parameters) must be known to the compiler at compile time. Moreover, for resolving overloading Spad does not use actual type (which is known only at runtime), but only category of the type. This means that in most cases
compiler is able to resolve overloading at compile time (if it can not resolve some case the compiler simply uses first match, or signals error if it has insufficient information to find any mutch).
|
It not compiler weakness but the core of Spad design. You get example by taking any parametrized domain or package, like:
PolynomialToUnivariatePolynomial(x:Symbol, R:Ring): with
univariate: (Polynomial R, Variable x) ->
UnivariatePolynomial(x, Polynomial R)
== add
univariate(p, y) ==
q:SparseUnivariatePolynomial(Polynomial R) := univariate(p, x)
map(x1+->x1, q)$UnivariatePolynomialCategoryFunctions2(Polynomial R,
SparseUnivariatePolynomial Polynomial R, Polynomial R,
UnivariatePolynomial(x, Polynomial R))
since R is know only at runtime only at runtime it is known what Polynomial R is. Note: since Polynomial is a literal constructor Spad at compile time creates apropriate category ("category of Polynomial(R) with R being an arbitrary ring") and this categorty is used to determine available signatures. Also given:
p1 : Polynomial R
p2 : Polynomial R
Spad compiler knows that p1 and p2 are of the same type. But only at runtime it will compute the actual domain.
BTW: In simple natural examples it is possible to completely eliminate runtime types -- while compiler does not know types the code will run exactly the same for all values of paramaters. But for example conditionals based on types are computed at runtime and require actual types. To know types in places where they are really needed we need to compute types at runtime in many places where at first glance everything could happen at compile time.
Let me add that in cases where types are known at compile time (when you use constructors without parameters, like Boolean or Integer), the compiler uses types for optimization, but nevertheless the types are again computed at runtime (this may be considered compiler weakness, but actually there are good reasons to do this).
> > In given call place there may be several (or none)
> > visible definitions for given function. Each definition comes
> > from some domain or package.
>
> Ehm, Waldek, would you say that SPAD does not allow top-level functions
> that do not live in domains? For sure the interpreter allows that. I
> haven't tested putting a function in a .spad file, though.
>
ATM Spad compiler assumes that top level functions are constructors. But the simplest method to add top-level functions to language description is to add special "top-level domain". So assuming that each function live in a domain simplifies description whithout restricting possible usage.
> > Let me say that it may be hard for
> > programmer to predict which function will be used by the
> > compiler,
>
> I'd say that it must be predictable. Easily predictable. The compiler
> should NEVER guess and choose one function where it has serveral options
> to choose from. In such cases the compiler MUST throw an error. If it
> doesn't, I consider that a compiler bug.
>
Concerning guessing: I general I agree. But there are cases where choice does not matter and then making arbitrary choice is not bad (I do not know if such cases apply to overloading).
Concerning ability to easily predict: this is programmer responsiblity. IIUC one can encode any NP problem (like breaking AES) into overload resolution problem for current compiler. Making compiler closer to right theoretical model involves solving harder problems. While the method currently used is too stupid to handle "intersting" problems, it still should easily beat humans.
<rant>
Fact that compiler can do things which are hard for humans is not a reason to cirpple the compiler. For example I agreed that compiler signals error for anonymous functions without type declaration in cases which require search. This forces programmes to add declarations in tricky cases. But it also forces declarations in many cases which are obvious to humans. More general, trying to force clear progams bylanguage restrictions may easily backfire.
</rant> |
> It not compiler weakness but the core of Spad design. You get
> example by taking any parametrized domain or package, like:
Ah... you meant parametrization of domains. That's indeed tricky.
Even in
Foo(R: Ring): Category == with
foo: % -> %
Foo actually is a (parametrized) type (category). Now,
Bar(R: Ring): Foo(R) == add ...
defines another type (a domain) Bar that depends on a Ring R.
I still would have called that static. But, in fact, the actual concrete category like Foo(Integer) only exists at runtime. Still, the compiler can derive a lot from the parametrized formulation of the category.
Actually, Foo is not a category, but rather a function that (given a concrete domain for its parameter R) returns a category.
And Bar is not a domain, but rather a function that (given a concrete domain for its parameter R) returns a domain. Interestingly, here is that Bar is a function whose return type, i.e. Foo(R) (not only the value, i.e. Bar(R)) depends on the input parameter. That is know under the name "dependent types" and is not often found in any programming language.
Also note that in the definitions of Bar and Foo, the parameter must be of type Ring, so it will already be detected at *compile-time* that Foo(String) is not a valid type since String does not satisfy the Ring properties.
> Concerning guessing: I general I agree. But there are cases where
> choice does not matter and then making arbitrary choice is not
> bad (I do not know if such cases apply to overloading).
Only, if the resulting function is exactly the same, I would agree, since then guessing does not matter. (It's actually not guessing anymore.) But if there are cases when there are two functions that do the same thing, the compiler should complain that it doesn't know what to choose. Why I want that behaviour is that the functionality of the cases might be the same, but they may differ in complexity.
I don't think it is a good idea to give up control over complexity of algorithms. But maybe you meant something else. Do you have a concrete case?
> Concerning ability to easily predict: this is programmer responsiblity.
> IIUC one can encode any NP problem (like breaking AES) into
> overload resolution problem for current compiler. Making compiler
> closer to right theoretical model involves solving harder problems.
> While the method currently used is too stupid to handle "intersting"
> problems, it still should easily beat humans.
>
> <rant>
> Fact that compiler can do things which are hard
> for humans is not a reason to cirpple the compiler. For example
> I agreed that compiler signals error for anonymous functions
> without type declaration in cases which require search. This
> forces programmes to add declarations in tricky cases. But
> it also forces declarations in many cases which are obvious
> to humans. More general, trying to force clear progams by
> language restrictions may easily backfire.
> </rant>
Oh, I don't want to add restrictions to the language, I just want deterministic programs, i.e. programs whose result does not depend on the compiler implementation.
Why I am so much for explicit type declarations, is that it makes programs more easily understandable by humans. One doesn't have to grep through all the inheritance chains to find the corresponding export.
Maybe all would be easier with a good IDE that pops up a window with the corresponding type of the object under the mouse pointer. ;-) Who is going to write that?
|
Structured comments
Comments preceded by ++ have the following structure:
In function definition:
myFunction:(param1:aType1,param2:aType2) -> aType
++ myFunction(param1,param2) gives such-and-such a result
++ param1 is such-and-such
++ param2 is such-and-such
++ and other free format comments
-- any comments that we don't want to go into user ducumentation such as todo list.
In category definition:
<<category MYSHORTNAME MyLongName>>=
)abbrev category MYSHORTNAME MyLongName
++ Author: MyName
++ Date Created: month year
++ Date Last Updated: month year
++ Basic Operations:
++ Related Constructors:
++ Keywords: whatever
++ Description:
++ Category of whatever, allows us to model whatever
++
++ References:
++ http://www...
Debugging SPAD
I have put some information about my attempts to debug Spad programs here.
References
The quotes on this page are from a discussion on the FriCAS forum here the following people gave very helpful and informative answers to my questions on this topic:
- Waldek Hebisch
- Ralf Hemmecke
- Martin Rubey
- Arthur Ralfs
Obiously I claim no rights to their work, I just quote them here to make sure that the information is not lost or hard to find.
Further Reading
SPAD syntax .
This site may have errors. Don't use for critical systems.




