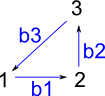This is a continuation of the tutorial for the graph theory code which starts here. If you have not already installed and loaded the code from 'graph.spad' then you first need to follow the instructions on that page.
On this page we explore the methods for combining the graphs, these include:
- "+":(%,%) -> % Sum : disjoint union of nodes with arrows from appropriate input
- merge:(%,%) -> % Sum : union (not necessarily disjoint) of nodes with arrows merged in from appropriate input, if arrow exists from both inputs then it will be duplicated.
- "*":(%,%) -> GRPHPROD Tensor product : the tensor product G*H of graphs G and H is a graph such that the vertex set of G*H is the Cartesian product V(G) × V(H); and any two vertices (u,u') and (v,v') are adjacent in G × H if and only if u' is adjacent with v' and u is adjacent with v.
- cartesian:(%,%) -> GRPHPROD Cartesian product: the vertex set of G o H is the Cartesian product V(G) × V(H) and any two vertices (u,u') and (v,v') are adjacent in G o H if and only if either u = v and u' is adjacent with v' in H, or u' = v' and u is adjacent with v in G.
- ~ The complement or inverse of a graph.
This page contains the following examples:
Simple Example
First we just construct a few types and macros to work with:
(1) -> GS := DirectedGraph(String)
(1) DirectedGraph(String)
Type: Type
(2) -> OBJT ==> Record(value:String,posX:NNI,posY:NNI)
Type: Void
(3) -> ARRW ==> Record(name:String,arrType:NNI,fromOb:NNI,_
toOb:NNI,xOffset:Integer,yOffset:Integer,map:List NNI)
Type: Void |